beskonacna kompresija - konacno resenje

da ponovim, po nepisanom pravilu to se zove PS. od eng. Post Scriptum

Sve ispred cega sam napisao npr. tumaciti kao na primer: "da sam ga nasao na npr. 175-om mestu se vise odnosilo na to kad ga nadjem kako cu da upamtim gde sam ga nasao tj. da dojavim generatoru da je na tom i tom mestu u nizu fajlova iste velicine i da to na neki nacin uspem da upamtim do sledece potrebe za tim podatkom tj. "regenerisanja" fajla. Lako je za fajl od 10 bita odrediti gde je to tacno. A kad budem pozeleo da koristim primer sa fajlom od 1GB? Hocete i onda brzo da mi dojavite na kom se on mestu tacno nalazi? Ne mislim da fajl koji sam takodje "lupio" samo primera radi na 175-om mestu, znam da je na 210-om. U medjuvremenu sam objasnio i kako to nameravam da zapisem. A narocito kako to nameravam da zapisem za vece fajlove.

---

Ok, ako tako cvrsto verujes u to, probaj da to implementiras - videces da jednostavno nece raditi - jer ce ti za vecinu simbola trebati vise prostora da ih smestis i opises nego u originalu.

Svaki signal (konacni niz karaktera da se ogranicimo) ima jednu vrednost koja se zove entropija, i koja oblikuje teoretski minimum sa kojim ta ista informacija moze da se opise.

Vidi, zakon o informaciji za informaticare ti je isto sto i zakon termodinamike za fizicare - danas se manje-vise uzima za nesto sto se uopste ne dovodi u pitanje, i to sa debelim razlogom.

---

MajorFatal, jedna stvar mi nije jasna kod tvog algoritma: kako se pravi generator za proizvoljni fajl?

Ja vec razmisljam da ovo nije neka provokacija ... Odgovorili su ti mnogi koji su itekako kompetentni u ovoj oblasti sa vrlo stalozenim i razumnim objasnjenjem, a ti i dalje po svom.

Svejedno, ako ne uspes nas da ubedis, obrati se Jutarnjem programu RTS1, tamo se obicno javljaju progresivni naucnici koji su izmislili auto-motor na vodu ili elektromotor bez rotora, pa ce se naci i za beskonacnu kompresiju mesta.

Javi kako je proslo

1. Koju vecinu simbola? Prilikom zapisivanja kompresovanog fajla nameravam da koristim deset cifara decimalnog sistema I b,B,M,G,T sto je jos pet, I jedan za razdvajanje dva zapisa u kompresovanom fajlu sve ukupno: 16. U slucaju pojave vrednosti iznad Tera za koju ne znam kako ce se zvati ali znam zasigurno da ce biti tacno 1024 Terabajta broj simbola mi se duplira sa 16 na 32 ali to nije nista u poredjenju sa povecanjem broja/velicine fajlova koje cu moci da kompresujem tj sa povecanjem sa T na 1024 T.

2.Mislim da ga nisam ugrozio, to sto neki tvrde da sve pokusavam da spakujem u 16 bajta ili 1 double znak je da nisu dobro procitali kako izgleda kompresovan fajl.

3. Potencijalni engine/program/implementacija ga pravi dinamicki. Ali ne u smislu da se ucitava iz nekakve dll biblioteke jer bi u tom slucaju za nase potrebe ta biblioteka 1. narasla do u beskonacno 2. bila nefunkcionalna – jos jedna pretraga, jos jedno uporedjivanje. Vec onako bas dinamicki tj. u hodu. Ako nista bar ima jednostavan zadatak napraviti generator(brojac) fajlova te I te duzine (N) koji ce poceti da generise fajlove od “prvog” tj. onog sa svim nulama pa sve do “prepoznavanja”. To je ujedno I jedan od retkih delova programa koji ostaje tu gde jeste tj. ne brise se po zavrsenom poslu.

4. I ne samo to odgovorili su mi I da “zipujem brojac” a posle se nisu potrudili da citaju dalje I da vide da sam u post-u od 07.02.2005. zipovo ono sto sam u svom prvom post-u nesretnim izborom terminologije nazvao brojacem. I to sam ga zipovo iz sve snage, bas je bio zgodan za zipovanje.

5. Nikog nista ne ubedjujem


6. Hvala za savet I za informaciju. Za auto-motor prvi put cujem, cuo sam za neke motore sa unutrasnjim sagorevanjem koji koriste alternativne izvore energije voda, plemeniti gasovi itd. Provericu.

---

Cekaj, opet mi nije jasan taj generator, zvuci kao da je brojac identican vrednosti fajla. Ako bi imao fajl koji izgleda ovako:

0x1234567812345678

Kako bi izgledao generator i koja bi bila vrednost brojaca?

Interesantno je to sto kaze za zapisivanje samo sa jedinicama. Ono kao, ako se 42. generisano fajl poklapa sa onim koji treba da se kompresuje to ce biti 111111111111111111111111111111111111111111 ili 42*1. Ono sto mu nije palo na pamet je da kad to uradi sa realnim fajlom imace zapis o broju jedinica istovetan originalnom fajlu sto samo znaci da ce povecati originalni fajl za dva bajta - "*1".

BTW, ako nekoga interesuje (skoro) beskonacna kompresija slika moze pogledati temu http://www.elitesecurity.org/tema/93788 sa programom koji sam dao u ovoj poruci. Nije lose procitati bar prvih nekoliko postova da se vidi o cemu se radi pre isprobavanja prorama.

Eto, 1440000*2^11520000 bajtova smesteno u 24KB

---

I ja bih rekao da ga nisi ugrozio, taman posla. Tvoj algoritam ima dva problema:

1) Jako je nepraktičan jer ima eksponencijalnu složenost.
2) Zapravo ne uradi ništa sa podacima, već je u najboljem slučaju samo permutacija na skupu svih datoteka zadate dužine N. Inverz se uvek lako nađe kao inverzna permutacija (u smislu da je lako napisati algoritam; samo treba sačekati jaaako dugo da se izvrši, da zanemarimo to sad), ali na žalost odnos veličina datoteke posle i pre kompresije ne može biti manji od 1.

Iako u novinama s vremena na vreme mogu da se pročitaju priče o neverovatnim algoritmima za kompresiju  (ovde se recimo vrti priča, izdaju knjige i pišu hvalospevi o izvesnom inženjeru koji je smislio neverovatan sistem za kompresiju, ali je umro dan pre nego što će u Filipsu (Philips) napraviti demo i potpisati ugovor vredan više milijardi čvrste valute; naravno i svi njegovi spisi i laboratorijski logovi su misteriozno nestali), kompresija nije nikakva mitologija. U pitanju je deo teorije informacija koja je vrlo dobro utemeljena matematička disciplina. Iako put do savršene kompresije nije zacrtan, tačno je poznato dokle ta savršena kompresija može da komprimuje datoteku. Ako recimo hoćeš da kompresuješ datoteku dužine N, jedini, ali zaista jedini način da to uspeš jeste da nekako znaš da se od svih mogućih datoteka dužine N ne mogu javiti baš sve datoteke. Pretpostavimo da nekako znamo koje se datoteke javljaju a koje ne javljaju. Onda napravimo prenumeraciju: jedan brojač koji broji preko svih datoteka koje mogu da se jave. 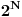Pošto njih ima manje od , brojač je manje dužine od polazne datoteke pa smo dobili kompresiju. To je tvoja osnovna ideja koja je gore izložena.

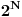
Problemi su: 1) to jako dugo traje, 2) ne postoji jednostavan način da znamo koja se datoteka može pojaviti a koja ne i 3) ako sigurno znamo da je svaka od datoteka moguća onda je apsolutno nemoguće išta kompresovati bez gubitaka. 1) je očigledno, jer je algoritam eksponencijalan. 3) je dokazao Šenon. 2) je problematično jer je praktično nemoguće napraviti brojač koji bi radio to što želiš. Zato se ljudi pomažu statistikom koja je u neku ruku surogat za univerzalno znanje o svim datotekama. Statistike naravno zavise od uzorka (podsećanje: statistika je funkcija na  skupu slučajnih promenljivih) a pošto su uzorci razni (slika, zvuk, datoteke, tekst itd), to imaš mnogo različitih statistika koje rade dobro u nekom ograničenom opsegu slučajeva.

Drugim rečima: ideja koju imaš je ispravna u principu, ali od nje nikada neće direktno da ispadne neki koristan algoritam — osim u slučaju da tačno znaš raspodelu svih datoteka — u kom slučaju je sasvim opravdano ono što si rekao da ti je bog došapnuo: on je verovatno jedini kandidat za takvo univerzalno znanje. (U računarskoj terminologiji se radije koristi izraz oracle, što izbegava religiozne konotacije).

Za kraj, da iskomentarišem onu Ivanovu referencu na Šenona i da bacim par linkova.

Nekad jeste lepo vratiti se i popiti vodu sa izvora, ali od Šenonovog vremena pojavili su se ljudi koji teoriju informacija objašnjavaju na daleko lepši i lakši način. (Na žalost pomenute knjige nema na Internetu a i malo je skupa.)

Od javno dostupnih knjiga za čitanje preporučujem knjigu (koja je izašla na hartiji ali je dostupna i online) Dejvida Mekkeja (David MacKay), koja odlično i matematički precizno opisuje mnoge probleme koji imaju veze sa teorijom informacija. Kompresija je samo jedna od njih.

Dejvid Mekkej je inače jedan od nekoliko ljudi koji su izmislili danas najefikasnije metode kodiranja tako da bi trebalo da zna šta priča, knjiga je puna slika i primera koji pokazuju čemu sve to služi i od nje možete da napravite 3 do 4 prilično zahtevna kursa za neke redovne, odnosno postdiplomske studije. Uzgred, tu se nalazi i problem Šeširdžija koji se pojavio u forumu Matematika pre nekoliko meseci.

Takođe možete pogledati i [url=http://lthcwww.epfl.ch/mct/index.php]knjigu u pripremi Ruedigera Urbankea[/url] koja se doduše bavi kodiranjem za prenos podataka (što je „druga strana medalje“ od kompresije) i takođe je [url=http://lthcwww.epfl.ch/papers/mct.ps]dostupna online[/url].

Samo da napomenem da nemam nameru da pridikujem kako treba ili ne treba prilaziti kompresiji podataka. Ako pogledate gore pomenute knjige i prošarate Internetom videćete da o kompresiji svakako nije rečena poslednja reč. Ali kao što ćete se složiti da nema smisla da budem stolar ako nemam alat — čekić, eksere, turpiju itd. — tako nema mnogo smisla baviti se i kompresijom podataka a da se ne pročitaju osnovne stvari.

f

In medias res-stari latini po zanimanju-balkanci
42*1 po novoj nomenklaturi bice 42bita=42/8=5celih bajtova+2bita=pisem u kompresovani fajl
B5b2..tj zapis koji u memoriji zauzima 4*8=32bita a posto smo krenuli od 42 bita a stigli do
32 tu bi negde trebalo da bude i teoretska granica nove kompresije. Inace ispravno
razmisljanje naveo sam primer sa nulama ali nije bitno da budu samo nule bitno je da fajl bude
"jednolican" tj. mogu i samo jedinice, a nije lose resenje 0101itd smanjuje drugi deo
kompresovanog fajla na pola (ako se potrudim da zapamtim samo nule ili samo jedinice)
resenja ima dosta ipak prvo do kojeg sam dosao izgledalo je ovako sve nule i jedna jedina
jedinica na mestu "prepoznavanja" pocetnog fajla. I slikom:

Ako trazim fajl:
10100110101

A na brojacu:
00000000000 0-Ovde pocinje "jednolicni" fajl tj fajl podlozan "staroj" kompresiji
00000000001 0
. 0
. 0
ga nadjem ovde: 0
10100110101 1-Jedna jedina jedinica tj. jedan jedini bit jedan u celom fajlu
. 0
. 0
a brojac da je 0
nastavio do kraja 0
bi stigo dovde: 0
11111111110 0
11111111111 0-Jednolicni fajl se zavrsava ovde.

Kasnije sam skapirao..sve ostalo!
HVALA!

---

Daklem, ispravka jedne uocene greske u racunu: posto sam se ranije u ovim postovima odlucio za 16 oznaka kojima cu kodovati zapis u kompresovanom fajlu, za tih 16 oznaka trebace mi po 4 bita za svaku a ne po 8 kao u prethodnom postu, dakle umesto 4*8 treba da stoji 4*4=16 bita iskoriscenih. te takodje: Posto je "jednolicni" niz dug 42 bita a sigurno se nalazi u rasponu do 2^N, 2^N mora biti (najmanje) 64 te ce jedan od najmanjih fajlova za koga ovo vazi biti "dug" 8 bita ili 1 bajt, ali taj svakako nece moci da bude kompresovan ovom metodom.

---

Pošto ja mislim da te niko ovde ne razume... hajde ti napravi kompresor i dekompresor i postani poznat i zaradi velike pare.. i mi ćemo onda da lupamo glavu kako smo oterali talenta sa foruma.

Ili će se desiti suprotno tj. shvatićeš šta pričaju ovi ljudi gore.

Eh, nemoj tako, niko ga ne juri sa foruma.

---

A šta, ako bi se, umjesto broja inkrementiranja fajla (koji zauzima koliko i originalni fajl, pa nema smisla) pamtila veličina fajla, MD5 string i redni broj fajla koji zadovoljava taj MD5 string? Broj fajlova TE veličine koji zadovoljavaju TAJ MD5 string ima mnogo manje od 2ⁿ gdje je n broj bita fajla.

Ovo je, naravno, samo teorija. U praksi bi ovakva kompresija i dekompresija, trajala veoma dugo.

Znači: 1 MB, 2f65bc103fafefd176bf588351f1525b, 12

Onda krenete od 000 ... 000 do 111 ... 111 i uzimate u obzir samo one fajlove koji imaju traženi MD5 string. Izaberete 12-ti po redu i to je traženi fajl.

---

Za MD5 se pretpostavlja da daje uniformnu raspodelu datoteka po prostoru ključeva. To znači ako je datoteka dugačka N bita, a MD5 ključ m bita (gde je m manje od N), za opis rednog broja svih datoteka će trebati tačno N-m bita. Drugim rečima, nema kompresije jer je potrebno m bita za MD5 i N-m za redni broj.

Da bi kompresija radila, moraš da izmisliš neki „digest“ za koji može da se dokaže da ne daje uniformnu raspodelu po prostoru ključeva, odn. da je očekivani broj bita za kodiranje manji od N-m.

Ideja ti nije pogrešna sama po sebi (kao ni ideja koju je dao OP), ali u oba slučaja nema nikakve garancije da će indeks da zahteva manje od N-m bita za pamćenje.

Kod OP-a je bilo m=0, kod tebe je m=160, ili koliko već bita ima MD5, ali priča je potpuno ista.

f

Sve me ovo podseca na matematicke glavolomke koje su imale cilj da zbune: lepo i logicno izgleda na prvi pogled, nakon par minuta razmisljanja znas da nije istina, ali treba otkriti gde je problem.

Znate sigurno za onu algebarsku caku da je 1=2 (a zapravo se u jednom koraku krati sa nulom), ili za malo starije ono sa integralima da je 0=1 (a zaboravimo konstantu koja se mora dodati) ....

Kada sam prvi put odgovarao na ovaj post, hteo sam dopisati:
... ako ikada sacekas da se ovaj algoritam izracuna.
Nisam, jer je toliko ocigledno da je inicijalni algoritam ovog posta toliko vremenski neefikasan.

Kasnije smo pricali samo o prostoru (efikasnosti kompresije), ali ne i o vremenu algoritma, makar su obe dimenzije jako bitne.

Cuo sam da je neko resio problem trgovackog putnika u realnom vremenu, makar mu treba nerealni prostor. well...

Sto se tice trgovackog putnika, jednom sam posetio prijatelja (tada je jos bio srednjoskolac) koji je resavao zadatke takmicenja mladih informaticara iz Madjarske, zadaci su mogli da se nose kuci. Jedan od zadataka je bio problem trgovackog putnika(?!). Pitam, kako si resio ovo? Kaze, lako je bilo, ali kada unese neki veci broj, kompjuter nesto previse razmislja ;) U zadatku je bilo naglaseno da algoritam treba da radi za 20 gradova. :)
Smatram ovo pozitivnim, oni koji su sastavljali test hteli su videti ko ce kako napasti ovaj zadatak, i do kojih ce zakljucaka doci.

Izvinjavam se na digresiji, ali, ako nista drugo, inicijalni post je izazvao mnogo interesantnih komentara, pa rek'o, bolje ovde da postujem, nego da pocinjem nove jalove teme.

A sto se tice kompresije: literature, hvala bogu ima. A kada se smisli algoritam --> na implementaciju, to zna isto biti uzbudljivo.

Proznajem da ne razumijem ovo... Ne bavim se kompresijom, ali mi je čitjaući ovu temu palo na pamet ovo što sam napisao u prethodnom postu.

Nedavno se Net-om proširila vijest da je neka grupa matematičara uspjela da slučajni niz 0 i 1 kompresuje u odnosu 1:10. To bi značilo da se svaki fajl (bez obzira koliko heterogen on bio) može bez gubitaka smanjiti 10 puta. Sigurno se ne radi o statističkom kodovanju koje ima drugačije ograničenje (nisam još polagao osnove telekomunikacija ;-) ).
Tada sam razmišljao o faktorijelima, npr. 123! daje mnogo veliki broj, pa bi to mogla da bude neka kompresija. Problem je što se ne može svaki veliki broj predstaviti kao faktorijel manjeg broja.
Možda nešto sa Gamma funkcijom? Lupam.

---

Onda taj niz nije slucajan ;) (think :-)

---

Sto znaci da bi brojem primena tog algoritma (prvo na pocetni fajl a onda i na rezultujuce fajlove) koji tezi beskonacnosti velicina kompresovanog fajla tezila nuli...
Svega toga ne bi bilo kada bi se ljudi prisetili barem srednjoskolske matematike...

Samo prenosim vijest :-)

---

Eo moje misljenje vezano za kompresiju.


Ne treba smisljati algoritam koji ce da dobro pakuje fajlove.

Treba smisljati fajlove koji ce da budu dobro pakovani...


over and out