[es] - Pitanje iz teorije skupova

pjesce

Član broj: 33057
Poruke: 11
*.panet.co.yu.

Profil

^{20.11.2004. u 17:21 - pre 248 meseci}

Da li bi neko mogao da mi objasni pojam ordinalnog broja malo elementarnije,ili da me uputi na neke korisne linkove iz teorije skupova?
Pretraživao sam na wolframu,ali nije mi bas najjasnije.

Odgovor na temu

Danica Porobic
Novi Sad

Član broj: 13847
Poruke: 28
*.194.EUnet.yu.

Profil

Re: Pitanje iz teorije skupova

^{20.11.2004. u 21:38 - pre 248 meseci}

Pogledaj ove skripte iz teorije skupova, u principu je objasnjeno na isti nacin kao i na mathworld-u, ali malo detaljnije i na srpskom ( ne znam da li ti ovo nesto znaci ):
http://www.im.ns.ac.yu/personal/madaraszr/Rozi-licno/skupovi.pdf

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu.

+64 Profil

Re: Pitanje iz teorije skupova

^{25.11.2004. u 19:17 - pre 248 meseci}

Ordinali služe za nabrajanje. Nešto kao generalizacija rednog broja. Evo šta kažu knjige:

- prvo pojam tranzitivnog skupa:
skup x je tranzitivan ako

povlači

šta ovo znači? ako x sadrži neki skup, onda sadrži i sve njegove elemente;

- onda se kaže da su ordinali tranzitivni skupovi koji su potpuno uređeni relacijom pripadanja; evo kako izgledaju (radi lakšeg zapisa a i kao potvrda intuicije, uvode se standardne oznake):

, ...,

, ...

Poredak ordinala se uvodi sa

Kardinali su ordinali koji se ne mogu preslikati 1-1 u neki manji ordinal. Svi konačni ordinali su kardinali.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dial.InfoSky.Net.

+2801 Profil

Re: Pitanje iz teorije skupova

^{26.11.2004. u 01:40 - pre 248 meseci}

Ordinali su tranzitivni skupovi koji su DOBRO uređeni relacijom

U teoriji skupova koja uključuje aksiomu regularnosti uslov dobre uređenosti skupa relacijom pripadanja je ekvivalentan uslovu linerane (ili potpune) uređenosti istog skupa istom relacijom. Sve ostalo što si napisao je OK.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

klupko
josip marin
Zagreb

Član broj: 19662
Poruke: 41
*.xnet.hr.

+1 Profil

Re: Pitanje iz teorije skupova

^{27.11.2004. u 16:39 - pre 248 meseci}

http://mapmf.pmfst.hr/~matko1/teorijaskupovateheksplorer.pdf

u poglavlju (mislim cetvrtom) o dobro uredjenim skupovima.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu.

+64 Profil

Re: Pitanje iz teorije skupova

^{27.11.2004. u 19:12 - pre 248 meseci}

Hm, interesantno. Kakav je značaj ordinalnih skupova u aksiomatici bez aksiome regularnosti? I kako se to odražava na pojam kardinalnog broja; ili na primer na hipotezu kontinuuma? I baš me zanima koje su to aktuelne teorije skupova bez aksiome regularnosti? Već smo ovde na forumu imali neku raspravicu o njenom značaju.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dial.InfoSky.Net.

+2801 Profil

Re: Pitanje iz teorije skupova

^{27.11.2004. u 19:47 - pre 248 meseci}

Ordinalni brojevi se mogu uvesti na više načina. U literaturi je prihvaćen ovaj Fon Nojmanov kao tranzitivnih skupova dobro uređenih relacijom

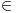
kao relacijom strogog poretka. Me]utim, pošto oni služe za nabrajanje (kao što si već napisao), suštin aim je u tome da se svaki skup može 1-1 preslikati u klasu svih ordinala (tj. ne postoji skup svih ordinala), da su dobro uređeni na neki način, i da za svaki ordinal

postoji skup svih ordinala koji su manji od

u tom uređenju.

Zato se njihova dobra uređenost uzima kao njihovo osnovno svojstvo (jer odražava njihovu suštinu), a onda se navode ekvivalentni uslovi. Ovaj sa linearnošću je važan kod modela Teorije Skupova, jer se na taj način dokazuje da je osobina "biti ordinal" apsolutna za sve tranzitivne modele. Inače, aksioma regularnosti važi u svm tranzitivnim mkdelima. Ipak, zbog prethodne primedbe takav način definisanja nije zgodan za nekoga ko prvi put uči Teoriju Skupova.

Teorija skupova bez aksiome regularnosti ima koliko i teorija skupova sa regularnošću. Radi se samo o tome da li je ta aksioma u spisku izabranih aksioma ili ne.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

pjesce

Član broj: 33057
Poruke: 11
*.panet.co.yu.

Profil

Re: Pitanje iz teorije skupova

^{28.11.2004. u 15:36 - pre 248 meseci}

Moram zaista svima da se zahvalim na pomoći;dobio sam par korisnih linkova i iscrpnih saveta,tako da mogu da nastavim svoj voyage kroz teoriju skupova.Takodje,nadam se da ću i ja biti u prilici da nekome nesebično pomognem kao i vi meni.Bravo za forum!!!

Odgovor na temu