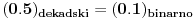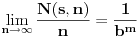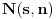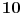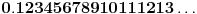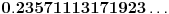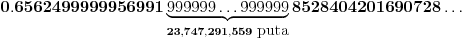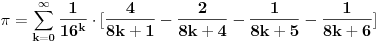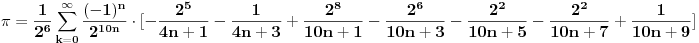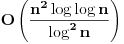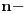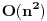[es] - Zanimljive raspodele u broju Pi

pirgos_madden
Pirgos Madden
Pirot

Član broj: 16752
Poruke: 322
195.252.107.*

Jabber: Programing
Sajt: www.pirot-mafia.co.sr

Profil

Zanimljive raspodele u broju Pi

^{23.11.2004. u 14:05 - pre 248 meseci}

Na sledecoj slici su na jednom grafikonu paralelno prikazane raspodele ukupnog broja pojavljivanja cifara u decimalama broja Pi do odredjene granice. Crna linija prikazuje raspodelu za uzorak od prvih 2000 decimala, crvena do 4000 decimale i td. do 16000 decimalnih mesta koja je obelezena onom cudnom zelenkastom bojom.

Kako se broj decimalnih mesta povecava sve vise se uocava pravilna struktura ove krive sa dva uocljiva "udubljenja" (nesto poput pisanog M samo malo spljostenog). Zar ne bi bilo logicno da ova raspodela bude prilicno ujednacena? Ovde to nije slucaj jer se na primer u primeru sa 16000 decimala cifra 4 se javlja cak 1670 puta dok se cifra 8 javlja svega 1543 (skoro 8 % razlika).

-I srusise se nasi divni snovi !!!
-NATO is bombing Serbia, a Yugoslavian republic, to stop the Serbs from forcing ethnic Albanians from Kosovo. Serb supporters sock it to NATO, U.S. Web sites. Magis says NATO headquarters won't launch an electronic counterstrike. "We want to show we're more civilized," he says. "We believe in freedom of speech." NATO is even discussing the possibility of hosting Serbian information on the Web so the Serbs can share their views.

Prikačeni fajlovi

pi-graf.JPG - 29.12k

Odgovor na temu

noviKorisnik
Dejan Katašić
Novi Sad

Član broj: 13216
Poruke: 4533
195.178.55.*

Sajt: www.novikorisnik.net

+5 Profil

Re: Zanimljive raspodele u broju Pi

^{23.11.2004. u 14:22 - pre 248 meseci}

... a potom isto mogu da se provere frekvencije cifara i u binarnom ili nekom drugom brojnom sistemu...

BoxUp
interesantna logička igra
Monty Hall paradoks - interaktivni demo

Odgovor na temu

Ivan Dimkovic

Administrator
Član broj: 13
Poruke: 16752
*.dip.t-dialin.net.

+7204 Profil

Re: Zanimljive raspodele u broju Pi

^{23.11.2004. u 14:56 - pre 248 meseci}

http://www.eveandersson.com/pi/precalculated-frequencies

in first 10,000,000 digits of pi
0 999440
1 999333
2 1000306
3 999965
4 1001093
5 1000466
6 999337
7 1000206
8 999814
9 1000040

Dakle, najmanji broj pojavljivanja je 99.82% najveceg broja, pa bi se slobodno moglo reci da je raspodela prilicno ujednacena :)

DigiCortex (ex. SpikeFun) - Cortical Neural Network Simulator:
http://www.digicortex.net/node/1 Videos: http://www.digicortex.net/node/17 Gallery: http://www.digicortex.net/node/25
PowerMonkey - Redyce CPU Power Waste and gain performance! - https://github.com/psyq321/PowerMonkey

Odgovor na temu

pirgos_madden
Pirgos Madden
Pirot

Član broj: 16752
Poruke: 322
195.252.107.*

Jabber: Programing
Sajt: www.pirot-mafia.co.sr

Profil

Re: Zanimljive raspodele u broju Pi

^{23.11.2004. u 16:59 - pre 248 meseci}

Citat:

noviKorisnik: ... a potom isto mogu da se provere frekvencije cifara i u binarnom ili nekom drugom brojnom sistemu...

Uzgred. . . moze li neko da pojasni kako se brojevi sa decimalama mogu prevesti u neki drugi brojni sistem sistem?

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
*.dialup.blic.net.

+197 Profil

Re: Zanimljive raspodele u broju Pi

^{23.11.2004. u 22:59 - pre 248 meseci}

Ajde malo to sredi pa prikaži u binarnom brojnom sistemu.
Napravi graf ovisnosti jedinica o broju cifara broja pi.
Ako nije 0:1 fifti fifti ,e onda ćemo se zabrinuti jer tu
ima nekog đavoljeg posla.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

pirgos_madden
Pirgos Madden
Pirot

Član broj: 16752
Poruke: 322
195.252.107.*

Jabber: Programing
Sajt: www.pirot-mafia.co.sr

Profil

Re: Zanimljive raspodele u broju Pi

^{24.11.2004. u 16:09 - pre 248 meseci}

Pa ok, moze to ali kako da pretvorim u binarni sistem broj sa decimalama? Da lepo uzmem svaku cifru pa pretvorim u binarni - mada sumnjam da ce se tako dobiti nesto sto nije fifti-fifti?

_{[Ovu poruku je menjao Bojan Basic dana 29.11.2004. u 13:48 GMT+1]}

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
*.dialup.blic.net.

+197 Profil

Re: Zanimljive raspodele u broju Pi

^{29.11.2004. u 12:12 - pre 248 meseci}

Broj "pi" možeš napisati u binarnom sistemu ovako:11.001001......itd.
a prevod ovoga u dekadski ide ovako: pi=1*2+1*1+0*1/2+0*1/4+1*1/8+0*1/16+0*1/32+1*1/64+....itd.
Odavde se vidi i kako dekadski decimalni broj prevodimo u binarni sa
mjestima iza zareza.

_{[Ovu poruku je menjao Bojan Basic dana 04.07.2005. u 22:42 GMT+1]}

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

Shadowed
Vojvodina

Član broj: 649
Poruke: 12881

+4827 Profil

Re: Zanimljive raspodele u broju Pi

^{29.11.2004. u 12:18 - pre 248 meseci}

Koliko se ja secam dekadni u binarni ide ovako:
Ceo deo uobicajeno, to verovatno svi znaju.
Razlomljeni deo mnozis sa dva;
Ako je dobijeni broj manji od 1 pises nulu
Ako je dobijeni broj veci ili jednak 1 pises 1, oduzimas od dovijenog broja 1
Ako krajnji broj nije 0 ponavljas ceo postupak.

Nebojsa Milanovic:
-Trumpa smatram vrhunskim predsednikom i voleo bih da živim u državi na čijem je on čelu
-Rusija ne laže, ne vodi osvajačke ratove
-Trump je svetla tačka u USA blatu
-Elon Musk, možda najpametniji i najtrezveniji Amerikanac

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
*.dialup.blic.net.

+197 Profil

Re: Zanimljive raspodele u broju Pi

^{29.11.2004. u 23:12 - pre 248 meseci}

Citat:

Shadowed: Razlomljeni deo mnozis sa dva;
Ako je dobijeni broj manji od 1 pises nulu
.

Ok.Vrijednost pozicionog mjesta je potencija baze 2.Dakle iza zareza
(jedinice) slijede 2^(-1) ili 1/2 itd.
Ali nije ovdje o tome riječ.Pirgos je napravio graf distribucije cifara
broja "pi" i na neki način sugerira da tu postoji izvjesna zakonitost.
A onda odjednom se pita kako se u binarnom sistemu piše broj
manji od jedan.Bez ikakve zle namjere htio sam mu samo malo
pomoći iako je o tome već bilo par tema.

I kao što Shadowed reče:

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dialup.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Zanimljive raspodele u broju Pi

^{04.07.2005. u 02:25 - pre 241 meseci}

Ajde da kažem reč-dve na ovu temu. Suština je da stvar nije ni blizu tako prosta kao što se čini.

Prvo uvodimo pojam „normalan broj“. Za neki broj ćemo reći da je „normalan u osnovi

“ ako za svaki prirodan broj

i za svaki niz cifara

dužine

važi

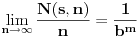
, gde

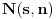
predstavlja broj pojavljivanja niza cifara

u prvih

cifara datog broja (u osnovi

). Broj je „apsolutno normalan“ (ili samo „normalan“) ako je normalan u svim prirodnim osnovama.

E sad, ovo što si ti rekao:

Citat:

pirgos_madden:
Zar ne bi bilo logicno da ova raspodela bude prilicno ujednacena?

predstavlja otvoren problem i jedan od najistraživanijih (ako ne i najistraživaniji) vezanih za broj

, tj. da li je

normalan broj (ili, specijalan slučaj, da li je normalan u bazi

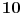
). Dokle su matematičari stigli sa ovim pitanjem? Pa, ne baš daleko reklo bi se — još uvek nije poznato čak ni to da li se sve cifre javljaju beskonačan broj puta!

Inače, jako malo stvari je poznato u vezi sa normalnim brojevima. Njih je definisao Borel 1909. godine, i dokazao da su skoro svi realni brojevi normalni — „skoro svi“ u smislu da je Lebegova mera skupa abnormalnih brojeva (brojeva koji nisu normalni ni u jednoj bazi) jednaka

. Ova teorema pokazala je egzistenciju normalnih brojeva, ali je tek Sjerpinjski (Sierpiński) 1917. dao primer konstrukcije normalnog broja. Međutim, problem njegove konstrukcije je što broj ne može biti eksplicitno izračunat — tek 2002. godine su Bečer (Becher) i Figera (Figuera) preformulisali konstrukciju Sjerpinjskog tako da je njegov broj sada moguće izračunati. Još jedna zanimljivost je da su Bejli (Bailey) i Krandal (Crandall) 2001. godine postavili hipotezu da je svaki iracionalan algebarski broj normalan, i za sada se ne zna kontraprimer ali ne zna se niti jedan takav broj!

Nešto bolja situacija je sa normalnim brojevima u bazi

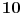
, dva verovatno najpoznatija (a i najjednostavnija) su Čampernounova (Champernowne) konstanta (

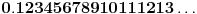
— prirodni brojevi pisani jedan za drugim) i Kopland—Erdeševa (Copeland—Erdős) konstanta (

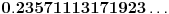
— prosti brojevi pisani jedan za drugim). Ipak, jedini za sada poznati normalni brojevi u nekoj bazi su tako veštački konstruisani.

Možda vredi pomenuti i „one druge“ — abnormalne brojeve. Za početak, očigledno je svaki racionalan broj abnormalan. Greg Martin je 2001. godine objavio svoju konstrukciju iracionalnog abnormalnog broja. Rekao je da se njegova konstrukcija lako može generalizovati i tako dobiti neprebrojivo mnogo abnormalnih brojeva, a broj koji je on analizirao počinje sa

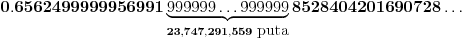
Odoh ja u oftopik, ali možda i ovo nekom bude zanimljivo.

_{[Ovu poruku je menjao Bojan Basic dana 13.10.2006. u 20:13 GMT+1]}

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

JustUser
Dragan Sataric
Beograd

Član broj: 62313
Poruke: 10
147.91.184.*

Profil

Re: Zanimljive raspodele u broju Pi

^{04.07.2005. u 15:35 - pre 241 meseci}

Za pitanje normalnosti broja su zanimljive formule koje omogućuju računanje n+1 cifre broja pi bez računanja prethodnih n cifara.
Takva je Bailey-Borwein-Plouffe formula

a postoji i Bellardova brže konvergirajuća formula

i još poneka formula...

ali se one odnose na računanje u bazi sa osnovom 2,4,16 (čak i 1024) ali ne postoji za dekadni sistem nijedna takva formula.
Mnogi su istraživali normalnost koristeći činjenicu da se proizvoljna cifra može "izvući" nezavisno iz niza cifara i odrediti pravilnost njenog pojavljivanja. Do danas ovi pokušaji nisu dali rezultat. I da jeste važili bi samo za heksadecimalne cifre.

Just another f***in forum writer.

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dialup.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Zanimljive raspodele u broju Pi

^{04.07.2005. u 23:50 - pre 241 meseci}

Citat:

JustUser:
ali ne postoji za dekadni sistem nijedna takva formula.

Tačno, ali postoji algoritam koji u (vrlo razumnom) vremenu

računa

tu cifru. Pronađen je 2003. godine, a do tada najefikasniji je bio vremena

. Da ne dužim puno, koga interesuje neka pročita prikačeni PDF.

_{[Ovu poruku je menjao Bojan Basic dana 05.07.2005. u 00:57 GMT+1]}

Ljubičice crvena, što si plava kô zelena trava.

Prikačeni fajlovi

nthdecimaldigit.pdf - 159.79k

Odgovor na temu