Lako se dokazuje da taj zadatak zapravo i nema rešenje. Označimo onoga ko uvek govori istinu sa +, onoga koji uvek laže sa -, a onoga ko ponekad laže, a ponekad govori istinu sa *. Neka nam na primer +*- označava da prvi uvek govori istinu, a treći uvek laže. Imamo sledećih šest mogućnosti:
1. +-*,
2. +*-,
3. -+*,
4. -*+,
5. *+-,
6. *-+.
Bez umanjenja opštosti možemo pretpostaviti da smo prvo pitanje postavili prvoj osobi. Koji god da smo odgovor dobili, ne možemo eliminisati mogućnosti 5 i 6. Dakle, neka je A skup mogućnosti koje nam ostaju ako smo dobili odgovor "da", a B skup mogućnosti koje na ostaju ako smo dobili odgovor "ne". Tada unija ta dva skupa uključuje svih šest mogućnosti, pri čemu se peta i šesta mogućnost nalaze u preseku ta dva skupa. Odatle sledi da ili oba skupa uključuju po tačno četiri mogućnosti, ili barem jedan od tih skupova uključuje barem pet mogućnosti.
U drugom slučaju nema rešenja. Zaista, recimo da skup A ima bar pet elemenata. Tada u slučaju da smo na prvo pitanje dobili odgovor "da", ne bismo mogli sa sigurnošću da utvrdimo ko je ko jer nam ostaje barem pet mogućnosti, a imamo samo četiri moguća odgovora na praostala dva pitanja (oba puta "da"; prvi put "da", a drugi put "ne"; prvi put "ne", a drugi put "da"; oba puta "ne"). Slično se dokazuje da ne možemo sa sigurnošću utvrditi ko je ko i u slučaju kada skup B ima barem pet elemenata.
Pretpostavimo da oba skupa A i B imaju po četiri elementa. Ukoliko bismo ponovo postavili pitanje prvom čoveku, ponovo ne bismo mogli da eliminišemo mogućnosti 5 i 6 bez obzira kakav odgovor dobijemo. Razmotrimo slučaj da smo na prvo pitanje dobili odgovor "da". Preostali slučaj se razmatra sasvim slično. Neka je C skup mogućnosti iz skupa A koje nam ostaju u slučaju pozitivnog odgovora na drugo pitanje, a D skup mogućnosti, takođe iz skupa A, koje nam ostaju u slučaju negativnog odgovora na drugo pitanje. Kako je
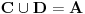
i mogućnosti 5 i 6 se nalaze u preseku skupova C i D, barem jedan od tih skupova mora imati najmanje tri elementa, pa u slučaju odgovora na drugo pitanje koji odgovara tom skupu nećemo moći trećim pitanjem da odredimo ko je ko, jer imamo barem tri mogućnosti, a samo dva moguća odgovora.
Stoga drugo pitanje moramo postaviti nekom od preostale dvojice. Bez umanjenja opštosti možemo pretpostaviti da je drugo pitanje postavljeno drugom čoveku. Oba skupa A i B imaju po četiri elementa i pritom barem jednom od njih pripada barem jedna od mogućnosti 2,4. Bez umanjenja opštosti možemo pretpostaviti da skupu A pripada jedna od tih mogućnosti. U slučaju da smo dobili pozitivan odgovor na prvo pitanje, ponovo nećemo moći tu mogućnost (2 ili 4 u zavisnosti od toga koja pripada skupu A) da eliminišemo bez obzira kakav odgovor dobijemo na drugo pitanje. Neka je E skup onih mogućnosti iz skupa A koje nam preostaju u slučaju pozitivnog odgovora na drugo pitanje, a F skup mogućnosti iz skupa A koje nam preostaju u slučaju negativnog odgovora na drugo pitanje. Ti skupovi nisu disjunktni (oba sadrže bar jednu od mogućnosti 2,4) i unija im ima četiri elementa, pa opet bar jedan od njih mora imati bar tri elementa, pa u slučaju odgovora na drugo pitanje koji odgovara tom skupu, na osnovu trećeg pitanja nećemo moći sa sigurnošću da utvrdimo ko je ko.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.