Srodne teme

20.07.2002. Kernel modules i prevodjenje Linuxa
14.08.2002. Generisanje slučajnog niza brojeva
27.10.2002. Digitalna elektronika
15.04.2006. kompresija BIN brojeva
11.12.2002. Skriptovi u dva thread-a
26.04.2005. Softver za prevodjenje
25.01.2003. Ponuda: Java programer za prevodjenje VB koda
10.06.2003. draw modal ?!?!
07.03.2010. konverzija fontova za XP
13.09.2004. Lista brojeva u Wordu

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

[es] :: Matematika :: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

[ Pregleda: 7875 | Odgovora: 15 ] > FB > Twit

Autor

Dream on
One way street

Član broj: 34418
Poruke: 9
*.mobtel.com

Profil

konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{14.09.2004. u 22:04 - pre 251 meseci}

Dakle imam oktalni broj 142 sa osnovom 8 koji treba prevesti u dekdadni zapis odnosno u osnovu 10.

Obrazac je sledeci:

1*8 (2) + 4*8 (1) + 2*8 (0) = 98

P.S. Ovi brojevi u zagradi (x) znaci da je to stepen

To mi je jasno, ali ne znam kako se odredjuje koji je broj iz kog sistema, oktalni, dekatni (znam za binarni jer su sve 0 i 1) ali mi nije jasno.
Primer: Broj 44446666 iz osnove 8 prevesti u osnovu 16 (to je vec onaj hexadecimalni oblik jer ima 16)

Ili ovo: 310 iz osnove 8 u 7

Onim obrascem sa pocetka poruke bilo bi ovako: 3*8 (2) + 1*8 (1) + 0*8 (0) a to je = 200 ali u kom sistemu? Oktalnom sa osnovom 8 jer sam mnozio sa 8?
Ili je ovde mozda trebalo da se mnozi ne sa 8 nego sa trazenom osnovom 7? To me zbunjuje.

Ako je neko raspolozen da mi napise objasnjenje, mnogo bi mi znacilo. HVALA!

Odgovor na temu

Shadowed
Vojvodina

Član broj: 649
Poruke: 12881

+4827 Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{14.09.2004. u 22:48 - pre 251 meseci}

Ovo sto si ti uradio pri prevodjenju 8->7 nije dobro. Zapravo si preveo na dekadni sistem.
Postoji generalna formula za prevodjenje iz bilo kojeg u bilo koji sistem ali je vrlo komplikovana za rad pa se sve to radi tako sto se najpre prebaci u dekadni (onako kako si napisao na pocetku) pa zatim u zeljeni sistem.
Stvar je u tome sto je potrebno selobrojno deliti broj sa osnovom sistema u koji pretvaras i zapisati ostatak. Postupak ponavljas sve dok ne dodjes do nule a zatim cifre koje si dobio kao ostatak zapises u obrnutom redosledu. Ali, ono sto je problem je to sto trebas da delis u tom osnovnom sistemu a to ljudi nisu navikli. Pokusaj da broj 137₈ delis u oktalnom sistemu (treba da dobijes 15₈ sa ostatkom 4).
Zato se prvo pretvara u dekadni sistem pa onda deli sa osnovom trazenog sistema.

Naravno, za deo posle zareza je drugaciji sistem ali mislim da ti to ne treba :).

Nebojsa Milanovic:
-Trumpa smatram vrhunskim predsednikom i voleo bih da živim u državi na čijem je on čelu
-Rusija ne laže, ne vodi osvajačke ratove
-Trump je svetla tačka u USA blatu
-Elon Musk, možda najpametniji i najtrezveniji Amerikanac

Odgovor na temu

Dream on
One way street

Član broj: 34418
Poruke: 9
*.mobtel.co.yu

Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{15.09.2004. u 00:38 - pre 251 meseci}

Hvala puno na pomoci, malo mi je sada jasnije :)

Dakle, broj 310 iz osnove 8 treba prevesti u osnovu 7. Prvo prevodim na dekadni sistem tako sto koristim obrazac: 3*8 (2) + 1*8 (1) + 0*8 (0) = 200 dekadno

E sad, posto treba da bude u osnovi 7, tek sada dekadnu vrednost delim sa trazenim sistemom, o ovom slucaju 7.

Citat:

Stvar je u tome sto je potrebno selobrojno deliti broj sa osnovom sistema u koji pretvaras

Sto bi bilo: 200 / 7 = 28.5714

Valjda bi tako trebalo? Jos da vidim sa tim ostatkom kako cu... :(

Citat:

i zapisati ostatak. Postupak ponavljas sve dok ne dodjes do nule a zatim cifre koje si dobio kao ostatak zapises u obrnutom redosledu.

Znaci zapisem 0.5714 OK. I sta s tim? Ovo mi nije jasno "dok ne dodjes do nule". Sta dalje da delim kada ne ostaje nista?

U svakom slucaju hvala puno na pomoci!

Odgovor na temu

cicika
Tijana Dojčinović
Software Developer, GroundLink
Zemun

Član broj: 24659
Poruke: 3104
*.smin.sezampro.yu.

+4 Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{15.09.2004. u 00:47 - pre 251 meseci}

Stani malo... Nije ostatak 0.5..., to je razlomljeni deo.
Misli se na ostatak celobrojnog deljenja:
28*7=196, do 200 fali 4 i to je ostatak.
Kanda smo zaboravili gradivo osnovne škole :)

_{Use The Force!}
_{“Who said anything about slicing you up? I just wanted to carve a little Z on your forehead — nothing serious.”}

Odgovor na temu

Dream on
One way street

Član broj: 34418
Poruke: 9
*.mobtel.co.yu

Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{15.09.2004. u 01:31 - pre 251 meseci}

Ih moja draga kad je bila osnovna skola.. Cak su i slike izbledele.... :)

Onda je bolje formulisati ovako: trazena osnova (u ovom slucaju 7) se dobija tako sto se izracuna koliko puta staje u prethodno dobijenu dekadnu vrednost (200). Sledi: 7 se u 200 nalazi 28 puta, od cega ostaje 4 i to je ostatak. Dalje, u ostatku 4 trazeni broj 7 se nalazi 0 puta, od cega ostaje 4 i dalje ne moz'. Dakle, rezultat je 404 u osnovi 7. Ako nisam opet nesto omasio :)

Odgovor na temu

lampica
Bg

Član broj: 31577
Poruke: 109
195.252.98.*

ICQ: 334198593
Sajt: www.skoladekart.com

Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{15.09.2004. u 07:15 - pre 251 meseci}

Citat:

Dream on:Dakle, rezultat je 404 u osnovi 7. Ako nisam opet nesto omasio :)

Dobro je...

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu

+64 Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{15.09.2004. u 07:32 - pre 251 meseci}

Jes, omašio si. Evo stiže jutarnja smena, da dokrajčimo ovaj tvrd oraj :)

Da, jeste dobar rezultat, ali si samo imao veliku sreću:
7 jeste u 200 28 puta, i ostatak jeste 4 ali ne gledaš sada koliko se 7 sadrži u ostatku nego u količniku, tj u 28. Pa razmisli, ostatak je uvek manji od delioca (valjda se tako kaže), tako da bi uvek u drugom krugu imao 0. Sada imaš nulu jer je 28 deljivo sa 7 - ostatak je 0 a količnik 4. Sada ide 7 u 4 nula puta i zapisuje se 4 kao prva cifra broja. Evo drugog primera:
352 = 50*7 + 2
50 = 7*7 + 1
7 = 1*7 + 0
1 = 0*7 + 1

Rezultat se čita unazad: 1012.

Odgovor na temu

neor
Nenad Orlovic

Član broj: 26828
Poruke: 74
*.metrohive.net

Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{15.09.2004. u 08:49 - pre 251 meseci}

Slicno se moze produziti i na decimalne brojeve. Na primer
0.32 * 7 = 2 + 0.24
0.24 * 7 = 1 + 0.68
0.68 * 7 = 4 + 0.76
0.76 * 7 = 5 + 0.32
0.32 * 7 = 2 + 0.24
...
pa se 0.32 u sistemu sa osnovom 7 pise 0.21452145...

Odgovor na temu

chupcko
Negde
Beograd

Član broj: 5560
Poruke: 1141

Sajt: www.google.com

+63 Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{15.09.2004. u 10:12 - pre 251 meseci}

Krajnje vreme je za neku teoriju, tipa svaki prirodni broj moze da se predstavi u obiliku

gde je

za

.

Naravno gde je

proizvoljan prirodni broj.

CHUPCKO

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu

+64 Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{16.09.2004. u 09:08 - pre 250 meseci}

Možemo to učiniti još interesantnijim. Setimo se zzzzadatka gde je težina k-te cifre bila k!. Hajde onda da krenemo ovako: (u daljem, skup prirodnih brojeva je N={0,1,2,...}) neka je dat

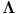
neprazan podskup partitivnog skupa prirodnih brojeva,

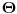
neprazan podskup skupa prirodnih brojeva i dve na funkcije

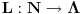
i

.
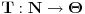
(Radi lakšeg praćenja, prvi je skup koeficijenata a drugi težina, određenog mesta u zapisu).
Reći ćemo da je prirodan broj n predstavljen u sistemu

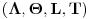
ako postoji izbor

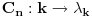
, gde je

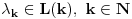
tako da važi:

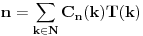
(C_n(k) je k-ta cifra a T(k) k-ta težina).

Brate al' sam ga zakomplikovao, boli me glava :) Ali, ne predajem se, idemo dalje.
Predstavljanje bi tebalo da bude jedinstveno i potpuno. To znači da izbor C_n postoji za svaki prirodan broj n i da ne postoji drugi sem tog. Pitanje je sada da li se samo na osnovu ovih osobina može doći do nečega konkretnijeg. Npr. da je T(k)<T(k+1), što bi bila veoma lepa osobina, iz koje bi moglo štošta drugo da se izvede. Dalje, možemo uvesti pojam dužina zapisa, jer je jasno da u konvergentnoj sumi beskonačno mnogo prirodnih (pozitivnih) brojeva svi članovi, počevši od nekog indeksa pa na dalje, moraju biti nula.
Imam još neke ideje, ali su one vezane za malo manje apstraktan slučaj, pa ih ostavljam za kasnije. Kad budem imao vremena, pokušaću ovo da razradim, a ko god je zainteresovan, nek' navali.

Odgovor na temu

Dream on
One way street

Član broj: 34418
Poruke: 9
*.14.EUnet.yu

Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{28.09.2004. u 03:06 - pre 250 meseci}

Citat:

darkosos: Jes, omašio si. Evo stiže jutarnja smena, da dokrajčimo ovaj tvrd oraj :)

Da, jeste dobar rezultat, ali si samo imao veliku sreću:
7 jeste u 200 28 puta, i ostatak jeste 4 ali ne gledaš sada koliko se 7 sadrži u ostatku nego u količniku, tj u 28. Pa razmisli, ostatak je uvek manji od delioca (valjda se tako kaže), tako da bi uvek u drugom krugu imao 0. Sada imaš nulu jer je 28 deljivo sa 7 - ostatak je 0 a količnik 4. Sada ide 7 u 4 nula puta i zapisuje se 4 kao prva cifra broja. Evo drugog primera:
352 = 50*7 + 2
50 = 7*7 + 1
7 = 1*7 + 0
1 = 0*7 + 1

Rezultat se čita unazad: 1012.

Hvala na pomoci! sad mi je jasno...
A kako za ovo. 44446666 iz osnove 8 prevesti u osnovu 16.

44446666 = 4*8 (7) + 4*8 (6) + 4*8 (5) + 4*8 (4) + 6*8 (3) + 6*8 (2) + 6*8 (1) + 6*8 (0) = ovo mi se cini da nece raditi, jer je broj ogromaan. :(

Ovo vec moze...
308 iz 9 u 11

3*9 (2) + 0*9 (1) + 8*9 (0) = 801

801 = 72*11 + 9
72 = 6*11 + 6
6 = 0*11 + 6
Rezultat je: 669

Darkosos hvala na forumulama i teoriji, svaka cast na znanju.. ali tesko da sam ista razumeo :) Cim vidim te alfe, mege, omege odma' mi se pije pivo i nema nista od matematike hehehe:)

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
*.dialup.blic.net

+197 Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{28.09.2004. u 16:47 - pre 250 meseci}

Pozicioni brojni sistemi su nastali tek kad je izmišljena nula.Rimljani
nisu mogli koristiti ovaj sistem (iako je i njihov pomalo pozicioni).

Evo jednog vizuelnog prikaza dva brojna poz. sistema.
Još ako neko zna pretvoriti N=5125 iz gornjeg u onaj donji?

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Prikačeni fajlovi

Brojni sistemi.GIF

Brojni sistemi.GIF - 13.33k

Odgovor na temu

neor
Nenad Orlovic

Član broj: 26828
Poruke: 74
*.metrohive.net

Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{28.09.2004. u 18:48 - pre 250 meseci}

5125 = ((5*3+1)*3 + 2)*10 + 5 = 505

7*9*8=504
znaci resenje je 1001 :)

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
*.dialup.blic.net

+197 Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{28.09.2004. u 22:47 - pre 250 meseci}

Čestitam Nenade!Brzo nema šta.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

Dream on
One way street

Član broj: 34418
Poruke: 9
*.mobtel.com

Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{29.09.2004. u 02:52 - pre 250 meseci}

Ljudi, zna li neko za hexadekadni sistem ovo..

Citat:

Dream on:
44446666 iz osnove 8 u osnovu 16.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu

+64 Profil

Re: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

^{29.09.2004. u 06:59 - pre 250 meseci}

I 8 i 16 su stepeni dvojke, pa možeš prvo u binarni. Svaka cifra oktalnog znači tri cifre binarnog:
44446666₈ = (100)(100)(100)(100)(110)(110)(110)(110)₂
a svake četiri cifre binarnog znače jednu cifru heksadecimalnog (naravno, krećeš od pozadi):
1001 0010 0100 1101 1011 0110₂ = 9 2 4 D B 6₁₆

Odgovor na temu

[es] :: Matematika :: konverzije (prevodjenje) brojeva iz jednog u drugi brojcani sistem?

[ Pregleda: 7875 | Odgovora: 15 ] > FB > Twit

Srodne teme

20.07.2002. Kernel modules i prevodjenje Linuxa
14.08.2002. Generisanje slučajnog niza brojeva
27.10.2002. Digitalna elektronika
15.04.2006. kompresija BIN brojeva
11.12.2002. Skriptovi u dva thread-a
26.04.2005. Softver za prevodjenje
25.01.2003. Ponuda: Java programer za prevodjenje VB koda
10.06.2003. draw modal ?!?!
07.03.2010. konverzija fontova za XP
13.09.2004. Lista brojeva u Wordu

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.