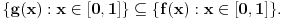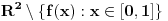Ja se sležem da je rešenje koje je priložio zzzz više nego dovoljno dobro i detaljno za ovo mesto. Međutim, ono je strogo govoreći matematički neprihvatljivo jer fale dokazi da će ravan bit podeljena na određen broj oblasti. Tu se pozvalo na očiglednost (crtež).
Problem tri kuće i tri bunara je problem da li je neorjentisan graf sa čvorovima A,B,C,D,E,F kod koga je svaki od čvorova A,B,C povezan sa svakim od čvorova D,E,F, planaran planaran pod pretpostavkom da drugih veza nema. Tu dakle treba znati šta je to planaran graf.
Put od tačke A do tačke B u ravni je bilo koja neprekidna funkcija segmenta [0,1] u ravan R
2 takva da važi f(0)=A i f(1)=B. Put je nesamopresecajući ako je 1-1. Nesamopresecajući put se još zove Žordanova kriva.
Teorema: Za svaki put f od tačke A do tačke B u ravni postoji nesamopresecajući put g od tako]e tačke A do tačke B u istoj ravni takav da je
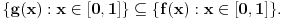
Graf je planaran ako se negovi čvorovi mogu predstaviti u ravni kao tačke, a veze kao puteve između takvih tačaka. Prema prethodnoj teoremi, uvek se može pretpostaviti da su putevi kojima su predstavljene veze između čvorova nesamopresecajući.
Zatvorena Žordanova kriva je funkcija f koje slika segment [0,1] u R
2 za koju važi f(0)=f(1) i koja je 1-1 na svakom od poluintervala [0,1), (0,1]. Skup A je otvoren ako za svaku tačku

postoji broj r>0 takav da sve tačke ravni koje su na rastojanju manjem od r od tačke a pripadaju skupu A. Prazan skup je takođe otvoren. Otvoren skup A je oblast ako se ne može predataviti kao unija dva neprazna disjunktna otvorena skupa. Poslednja osobina se inače zove povezanost.
Teorema o Žordanovoj krivoj: Za svaku zatvorenu Žordanovu krivu f, skup
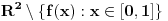
se sastoji od tačno dve disjunktne neprazne oblasti od kojih je jedna ograničena, a druga neograničena.
Ova teorema se još izražava rečima da svaka zatvorena Žordanova kriva deli ravan na dve oblasti. Ograničenu zovemo unutrašnjošću, a neograničenu spoljašnjošću te Žordanove krive. Prvi dokaz pomenute teoreme ponudio je Žordan 1887. godine, ali taj dokaz nije bio korektan. Prvi korektan dokaz datira iz 1905. godine i bio je izveden metodama Algebarske Toplogije. Na osnovnim sudijama Matematike na Matematičkom Fakultetu u Beogradu na predmetu Osnovi Geometrije se dokazuje poseban slučaj ove teoreme kada se zatvorena Žordanova kriva svodi na poligon (mnogougao). Ta teorema ima jedan od dužih dokaza koji su izloženi u udžbeniku Zorana Lučića za pomenuti fakultet. Potpun dokaz ove teoreme se može naći u udžbeniku Algebarske Topologije čiji je autor Džejms mankres (James Munkres).
Ovakve stvari je koristio zzzz u svom rešenju bez dokaza, pa taj dokaz nije strogo gledano matematički prihvatljiv. Ipak, njegovo rešenje bi bilo prihvaćeno na svakom takmičenju iz Matematike.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.




 Tri kuće i tri bunara
Tri kuće i tri bunara