Jednačina
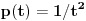
ima rešenja
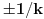
za
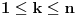
i ekvivalentna je jednačini
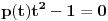
. Prirom je
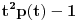
moničan polinom stepena
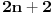
kome su koreni
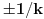
za
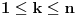
, pa je deljiv moničnim polinomom
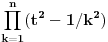
stepena

, pa je preostali činilac monični polinom stepena 2.
Dakle, za
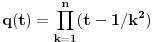
i neke realne brojeve

i

važi
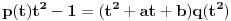
.
Pritom je

moničan polinom stepena

, odnosno za neke realne
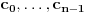
važi
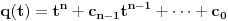
i
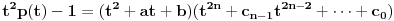
.
Upoređivanjem slobodnih članova i koeficijenata uz

na obe strane jednakosti dobijamo da je[/tex]
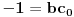
,
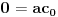
.
Obzirom na definiciju polinoma

, njegov slobodni član
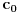
je
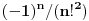
, pa je
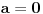
,
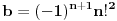
.
Dakle, preostala rešenja jednačine
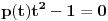
su rešenja jednačine
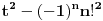
.
Za

neparno nema preostalih realnih rešenja, dok su za

parno preostala rešenja
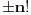
.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 prirodan broj i
prirodan broj i 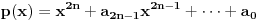 za neke realne
za neke realne 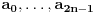 . Ako je
. Ako je 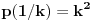 za sve cele brojeve
za sve cele brojeve  za koje je
za koje je 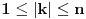 , naći preostala realna rešenja jednačine
, naći preostala realna rešenja jednačine 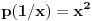 .
.