Zbir je
(*)
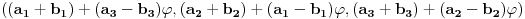
.
Neka su
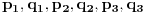
ma koji parni celi brojevi.
Tada vektor
(**)
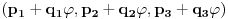
ima oblik prethodnog zbira za
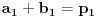
,
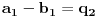
,
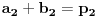
,
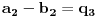
,
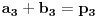
,
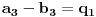
,
odnosno
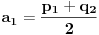
,
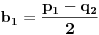
,
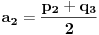
,
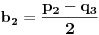
,
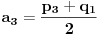
,
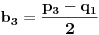
.
Brojevi
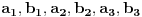
su celi kao polovine parnih brojeva. Dakle, na opisani način se može dobiti bilo koji vektor oblika (**), gde su
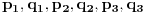
parni celi brojevi, odnosno dvostruka vrednost bilo kog vektora oblika (**), gde su
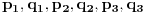
celi brojevi.
Izaberimo koordinatni sistem sa centrom u centru datog ikosaedra, takav da za neku pozitivnu konstantu

temena imaju koordinate
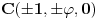
,
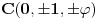
,
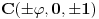
i neka je
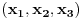
ma koji vektor.
Izaberimo cele brojeve
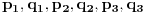
takve da važi
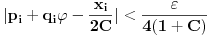
. Tada dvostruka vrednost vektora (**) odstupa od vektora
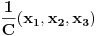
manje od
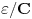
, dok odgovarajuća celobrojna linearna kombinacija vektora koji spajaju centar datog ikosaedra sa njegovim temenima odstupa od
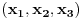
za manje od

.
Dokažimo da za ma koji iracionalan broj

važi da je skup
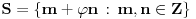
.
Ako sa
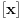
označimo najveći ceo broj koji nije veći od

, onda za niz
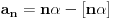
važi da je ograničen između 0 i 1 i da je
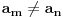
za
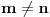
.
U suprotnom bi iz
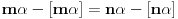
sledilo
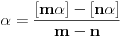
, što je u suprotnosti sa iracionalnošću broja

.
Svaki ograničen niz ima konvergentan podniz, pa se oduzimanjem bliskih različitih elemenata datog niza dobija da skupu

pripadaju proizvoljno mali pozitivni brojevi.
Neka je

ma koji realan broj i neka je

proizvoljno veliki prirodan broj. Neka su
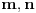
celi brojevi takvi da je
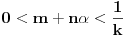
i neka je

najveći ceo broj takav da je
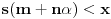
. Tada je
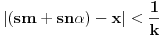
.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 i temenima
i temenima  . Dokazati da za svaku tačku
. Dokazati da za svaku tačku  i svako
i svako  postoje celi brojevi
postoje celi brojevi  takvi da važi
takvi da važi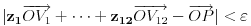 .
.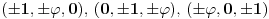 , gde je
, gde je 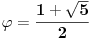 .
.