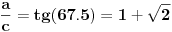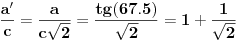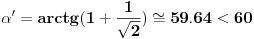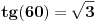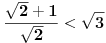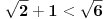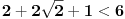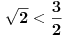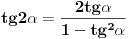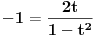Eh pa hvala, ne bih uspeo bez Vas, kaže geogebra 44,16 stepeni ...

Citat:
djoka_l: Nemoj da računaš sa float brojevima.
Evo ti link na matrice rotacije:
https://en.wikipedia.org/wiki/Rotation_matrix
Na slici si obeležio samo 2 tačke, a imaš na prvoj slici OSAM tačaka i centar kružnice.
Zaboga OZNAČI SVE TAČKE. Nađi koordinate. Izračunaj transformacije, i uglove. Nemoj da računaš sisnuse i kosinuse na 3 decimale, nego ti treba TAČNA pozicija tačke, recimo da j X koordinata 1*sin(pi/4). Onda nećeš da dobijaš greške zaokruživanja.
Ako više voliš, možeš da predstavih lik u kompleksnoj ravni, da se ne bi mnogo mučio sa trigonometrijom.
Kako a' može da bude 1.707 ako uzmeš da je prečnik opisane kružnice 1. Može da bude samo manje.
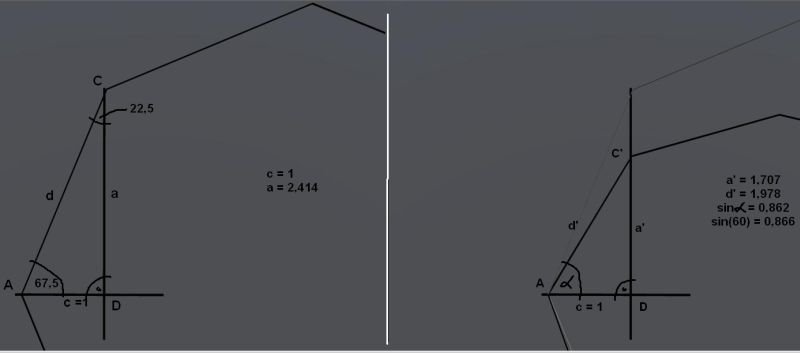
Matrice rotacije, kompleksna ravan .. to ne umem da primenim, ali hvala u svakom slučaju. a' je 1.107 jer sam za potrebe brze provere, lakšeg računa, usvojio da je c = 1 piše na slikama, i naravno na kraju nisam bio siguran da li su mi 0,04 pojele decimale ili ugao nije 120 :)
Citat:
B3R1: Pa dobro si uocio. U prvobitnom osmouglu vazi:
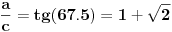
Dobro a/c = tangens, ali odakle to da je sve to jednako 1 + koren iz 2 ?
Citat:
Kada se osmougao rotira za 45 stepeni, tada se
a skracuje tacno sqrt(2) puta, pa je:
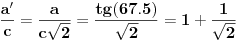
Ja množio sa sinus 45, dobro to je isto (valjda) :)
Citat:
djoka_l: To je, otprilike JEDINI način da se u ovom slučaju nešto izračuna (ali ne na tri decimale, nego onako kako je Beri uradio). Ovde ne možeš da upotrebiš dokazne postupke iz Euklidske geometrije, nego moraš da računaš, tj. da koristiš analitičku geometriju.
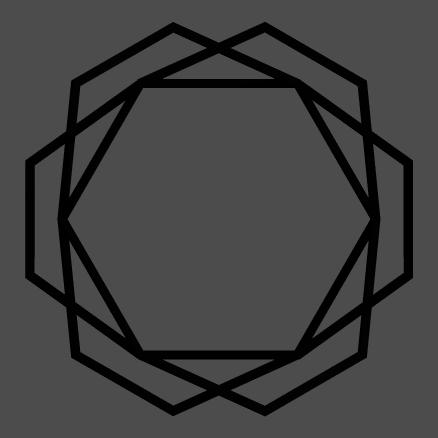
Spolješteni osmougaonik nije dobijen izometrijskom transformacijom.
U stvari, ti si prvo uradio izometrijsku transformaciju (rotaciju u 3D), ali si onda uradio PROJEKCIJU, a to više nije izometrijska transformacija, pa možeš da zaboraviš Euklida.
Ako može objašnjenje, zašto da zaboravim Euklida, valjda i projekcije podležu tim pravilima?
A dvanestougao? Je l isto pod 45 nije, verovatno svaki drugi ugao različit, a po 44,16 jeste, ili kako? :)
Nemoj da pricas?
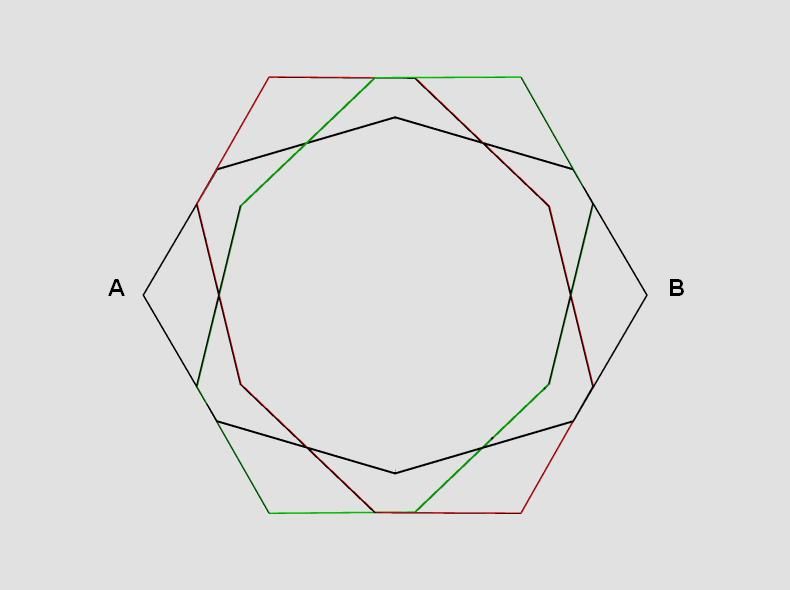




 Osmougao, dvanaestougao, šestougao ...
Osmougao, dvanaestougao, šestougao ...