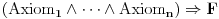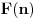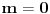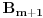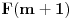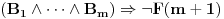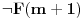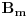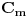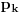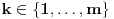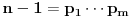Da li biti programer? Buducnost profesije

Re: Da li biti programer? Buducnost profesije 17.08.2020. u 23:59 · pre 75 meseci #861

@Nedeljko,

Pa u principu nemas izbora da li hoces ili neces da ides daleko, pozicija solipsizma je neizbezna, samo za svoju svest mozes biti, stvarno, siguran.

To ne mora biti nikakva prepreka, mozes komotno i da pretpostavljas da objekti koji lice na tebe poseduju svest slicnu tvojom, itd.

Sustina je da ne mozes biti siguran ni u prisustvo ili odsustvo svesti van svoje sopstvene. Zbog toga su sudovi o svesnoscu drugih objekata, ako mene pitas, suvisni.

Sto se kvantne mehanike tice, do redukcije dolazi kada posmatrac dobije znanje o rezultatu merenja.

Problem posmatraca (eksperimentatora) je, ocigledno, neresen bas kao sto jos nema odgovora na pitanje "gde" se nalazi granica izmedju aparata i posmatraca. Srecom nije neophodno naci odgovor na to pitanje (koje mozda nikada necemo naci ili ce odgovor biti takav da se nekima vrlo ne svidja) pa da sa kvantnom mehanikom moze da se racuna i da se koristi.

Ne znam kako bi bio siguran da stanje nisi redukovao ti a ne macka?

Uzgred, mozes da podelis izvor koji opisuje sta to tacno treba da zadovolji fizicki proces da dodje do redukcije? Mozda sam ja glup ili ne kapiram nesto, ali kako god gledao i sta god pokusao, od dekoherencije ne mogu da napravim posmatraca. Bez posmatraca cela stvar ne deluje da moze da funkcionise, bar meni.

Citat:

pctel
Kako se tacno ovo zna? Naprimer, covek moze da sanja da je leptir i da mase krilima, leti okolo, uziva u prirodi, vidi cvece, oseca vetar... Taj leptir tada zna da postoji njegova svest, a samim tim i on, ali nijedno od toga nije tacno.

Svesnost da postojis nije isto sto i verodostojnost signala koji ti stize iz okruzenja. Covek koji sanja da je leptir i dalje - sanja i sustinu njegove svesti cini subjektivni osecaj da postoji. To sto taj covek nije leptir ne menja cinjenicu da je svestan i kao dokaz za to moze koristiti fakat da sve vreme primecuje da postoji.

Potpis

DigiCortex (ex. SpikeFun) - Cortical Neural Network Simulator:
http://www.digicortex.net/node/1 Videos: http://www.digicortex.net/node/17 Gallery: http://www.digicortex.net/node/25
PowerMonkey - Redyce CPU Power Waste and gain performance! - https://github.com/psyq321/PowerMonkey

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 00:07 · pre 75 meseci #862

Pauza između dve poruke koje pravi moler je u proseku 3 dana (dok ne završi jedan stan). Programer može da napiše odgovor i posle mesec dana! Ako mene pitate, profesija budućnosti je moleraj! Kao moler vi ste umetnik i ne morate da brinete da će vas zameniti veštačka inteligencija.

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 00:12 · pre 75 meseci #863

Učeći matematiku naučio sam mnoge genijalne ideje, kojih se ja ne bih setio. Tu pada solepsizam. Neke ideje su u mom umu, a da je moj um bio suviše skromnih mogućnosti da dođe do njih. Dakle, u moj um su došle spolja. Do tih ideja je došlo neko inteligentno biće pre mene, dakle, moja svest nije jedina. Tu puca solepsizam, sad sam se setio.

Čuo sam da postoji bitna razlika između evolucije stanja u redukovanom, odnosno neredukovanom obliku, tako da se može proceniti kada je došlo do redukcije. Ako je došlo pre nego što sam ja pogledao, onda ga je mačka redukovala. E, sad, ja kvantnu fiziku ne znam, pa ne mogu da tvrdim.

No, ne moramo ići toliko daleko do neprihvatanja svesti drugih bića. Uvođenje razumnih pretpostavki je sasvim racionalno. Ni nauka, koja počiva na sumnji, ne može bez aksioma.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 00:48 · pre 75 meseci #864

Citat:

Ako moler okreči 3 stana mesečno i svaki naplati u proseku 500e to je 1500e mesečno. Ako radi samo jedan sloj, stan od 100 kvadrata može da okreči za 3 dana, što znači da programersku platu može da zaradi za 9 dana.

To je tako zato sto vec postoji molerska vestacka inteligencija koja radi tokom preostalih dana u mesecu, naprimer:
https://youtu.be/hm9ZSN37jVM

Kada programeri naprave vestacku inteligenciju koja moze da programira, tada ce i oni da rade 9 dana mesecno a ostatak da uzivaju.

Potpis

Samo ti sinko (administratore) radi svoj posao.

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 05:23 · pre 75 meseci #865

Mislim da sve sto je zivo ima neku svest. Voleo bih da vidim da neko napravi robota koji ce da imitira zivo bice...
Inace oci su ogledalo svesti..

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 07:15 · pre 75 meseci #866

Citat:

B3R1: Tako se i Kurt Gedel uhvatio u kostac sa matematickim dokazom da bog postoji ... bio je inace veliki vernik. Ta teorema koju je sebi pod stare dane postavio, pa pokusao da je dokaze matematicki - sve to ga je na kraju kostalo mentalne bolesti. Slicno je prosao i njegov prethodnik - Georg Cantor. Obojica su se zapravo bavili teorijom kontinuuma. Izgleda da ko se dohvati te oblasti matematike mahom sizne ... :-)

Kurt Gedel je oboleo iz sasvim drugih razloga.

Kada je 1933. godine Hitler došao na vlast, njegov uticaj se osećao i u Austriji, na Univerzitetu u Beču, gde je Gedel bio profesor. Pod tim uticajem su ukidana fundamentalna istraživanja, pa je Gedel skresan na privatnog docenta, što je neplaćeni profesor, koji može da se dogovori sa studentima koliko da ga plaćaju, ako ima zainteresovanih. Nakon toga, on odlazi za SAD.

1936. godine čuo je da je u Beču neki pro-Naci student ubio rukovodioca logičkog seminara koji je Gedel posećivao dok je bio u Austriji. Pošto je Trocki ubijen u Meksiku i zveketalo se širom sveta, Gedel se uplašio za sebe i dobio maniju gonjenja, od koje se izlečio, ali koja mu se kasnije ponovo vratila.

Kantor nije poludeo, nego je došao do kontraintuitivnog rezultata da postoje veće i manje beskonačnosti, zbog čega mu je njegov neprijatelj Leopold Kroneker napakovao smeštanje u ludnicu. Danas se po tom osnovu ne može niko proglasiti ludim.

Citat:

Branimir Maksimovic: Ostavio nam je ovo:

https://en.wikipedia.org/wiki/...el%27s_incompleteness_theorems

Mislim da je moj profesor matematicke logike to iskoristio da dokaze da ne postoji algoritam za dokazivanje valjanih formula, pa samim tim ni algoritam za pravljenje algoritama,
sto vodi u to da je AI nemoguc.

Zapravo, postoji algoritam koji ima sledeće osobine:

1. Za dati niz znakova utvrdi da li je ispravno formirana predikatska formula (parser).

2. Ako jeste, pokuša da dokaže njenu valjanost, pri čemu

a) Ako je ulazna formula valjana, algoritam uspe u tome u konačnom vremenu i stane. Ipak, nemoguća je procena koliko dugo treba čekati ako je ovo slučaj.

b) Ako ulazna formula nije valjana, onda radi neograničeno dugo.

To se zove poluodlučivost predikatskog računa. Primeri algoritama sa tim osobinama su:

Resolution in first order logic
First-order logic tableau

Ono što ne postoji je algoritam sa sledećim osobinama:

Zapravo, postoji algoritam koji ima sledeće osobine:

1. Za dati niz znakova utvrdi da li je ispravno formirana predikatska formula (parser).

2. Ako jeste, pokuša da ispita njenu valjanost, pri čemu

a) Ako je ulazna formula valjana, onda algoritam uspe da dokaže njenu valjanost u konačnom vremenu i stane.

b) Ako ulazna formula nije valjana, onda algoritam uspe da dokaže da ona nije valjana u konačnom vremenu.

Nepostojanje takvog algoritma se zove neodlučivost predikatskog računa.

Dokazivanje valjanosti je moguće ako je formula valjana.

Dokazivanje da formula nije valjana, ako je to slučaj, u opštem slučaju nije moguće.

Citat:

Shadowed: Postoji li negde online taj dokaz? Ja bih rado pogledao (ako uspem da razumem), ta oblast (AI) me veoma zanima. Da li je uradjen peer review?

To je danas klasika. Evo potrebnih linkova sa wikipedije, pa vidi šta ona linkuje.

Gödel's incompleteness theorems
Von Neumann–Bernays–Gödel set theory
Completeness and undecidability

Naravno, ima po ozbiljnim udžbenicima matematičke logike.

Ima više načina da se dokaže neodlučivost logike prvog reda.

Jedan je da se svakoj UR mašini i njenom ulazu pridruži predikatska formula koja je valjana akko je ta UR mašina za taj ulaz zaustavljiva.
Tako se dokazuje u knjizi "Matematička logika" autora Slobodana Vujoševića.

Drugi način je preko Gedelovih teorema nepotpunosti na primeru NBG teorije skupova, koja ispunjava uslove za Gedelove teoreme nepotpunosti, a ima konačan broj aksioma. Taj pristup se koristi u knjizi "Introduction to metamathematics" autora Steven-a Kleene-a.

Naime, pošto NBG teorija ima konačno mnogo aksioma i sve su formule prvog reda, formula $F$ teorije NBG je teorema te teorije akko je formula

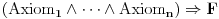
$({\mathrm{Axiom}_1}\land\cdots\land{\mathrm{Axiom}_n})\Rightarrow F$

valjana, pa ako postoji algoritam odlučivanja valjanosti formula, onda je teorija NBG odlučiva. Međutim onda bismo mogli da formulišemo i njeno neprotivrečno kompletiranje, a da postoji algoritam koji itvrđuje da li je nešto aksioma ili nije. Naime, postoji algoritamski izračinljiva funkcija koja prihvata prirodan broj na ulazu i na izlazu daje predikatsku formulu na jeziku NBG, tako da se svaka formula može dobiti za neki prirodan broj. 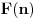Recimo da je $F(n)$ formula koja se dobija za prirodan broj $n$ na ulazu.

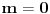
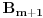
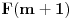
Onda treba da formulišemo koje formule prihvatamo kao dodatne aksiome. Naime, ako smo do nekog trenutka prhvatili $n$ aksioma $B_1,\dots,B_m$ , gde je na početku $m=0$ , onda se formula $B_{m+1}$ bira kao formula $F(m+1)$ ako formula

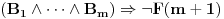
$(B_1\land\cdots\land B_m)\Rightarrow\lnot F(m+1)$

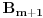
nije teorema teorije NBG, dok se u suprotnom formula bira da formula $B_{m+1}$ bude formula $\lnot F(m+1)$ .

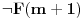
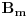
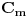
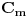
Uz sve te dodatne aksiome $B_m$ dobićemo popunu neprotivrečnu teoriju. Ekvivalentnu teoriju ćemo dobiti sa nizom aksioma $C_m$ gde je $C_m$ formula

$B_1\land\cdots\land B_m$ .

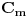
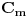
Dakle, NBG sa dodatnim aksiomama $C_m$ je takođe potpuna i neprotivrečna teorija. Međutim, tom slučaju postoji algoritam koji za datu formulu na ulaz proverava da li je aksioma. Naime, prvo proveri da li je to neka od NBG aksioma (njih ima konačno mnogo), pa ako nije, onda proverava da li je neka od $C_m$ formula. Mada ovih drugih ima beskonačno mnogo, izabrane su tako da po broju znakova budu sve duže, tako da će konačna provera biti dovoljna. 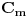Ako nisam našao datu formulu, a formula iz niza $C_m$ do koje sam stigao je duža od date formule, onda se ni naredne neće poklopiti jer su još duže.

Međutim, postojanje takvog kompletiranja teorije NBG je u suprotnosti sa Gedelovim teoremama nepotpunosti, pa je pretpostavka o odlučivosti logike prvog reda netačna, odnosno logika prvog reda je neodlučiva.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 08:12 · pre 75 meseci #867

Citat:

djoka_l: Recimo iskaz: Postoji najveći prost broj verovatno ne može da se ni dokaže ni ospori

Euklid je dokazao da prostih brojeva ima beskonačno mnogo.

Ako su $p_1,\dots,p_m$ svi prosti brojevi, onda je broj $n=p_1\cdots p_m+1$ složen, jer se razlikuje od svih od brojeva $p_1,\dots,p_m$ za koje je pretpostavljeno da su svi prosti. Zbog toga je broj $n$ deljiv nekim prostim projem, odnosno nekim brojem $p_k$ za neko $k\in\{1,\dots,m\}$ . Međutim, broj $n-1=p_1\cdots p_m$ je očigledno deljiv sa $p_k$ , pa je sa $p_k$ deljiv i broj $n-(n-1)=1$ , što svakako nije slučaj. Dobijena protivrečnost znači da skup prostih brojeva nije konačan.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 08:40 · pre 75 meseci #868

Posmatrač nije čovek nego mašina kojom se vrši merenje.
Tako da svest eksperimentatora sama po sebi ne utiče na posmatranu pojavu.
Na merenu pojavu svest eksperimentatora utiče posredno i to izborom metoda merenja i uslova odnosno okolnosti pod kojim se vrši merenje.
Do "kolapsiranja" stanja ne dolazi onda kad eksperimentator sazna za rezultat merenja
jer "kolapsiranje" nije prirodan proces već nesposobnost matematike da opiše prirodne pojave.
Mašina kojom se vrši merenje može da utiče na "kolapsiranje".
Čovek nema kognitivni kapacitet da spozna pojave iz mikro sveta onakve kakve jesu
nego pokušava da ih predstavi poznatim pojavama i fenomenima iz makro sveta.
Tu nastaje problem koji treba da reši na primer: koncept "kolapsiranje".

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 08:56 · pre 75 meseci #869

@pctel

Ti ovo nazivaš molerom?

Ovo čudo ne može samo ni da se popne uz stepenice da dođe do stana. Kako će da zaobilazi stvari? Jel ja treba da iznesem sve stvari da bi on mogao da kreči? Šta je sa nedostupnim prostorom pored ormara? Hoće li da izgletuje zid? Skine mrlje od komaraca? Postavi traku ispod plafona? Pomeša boju? Pogledaj samo prelaz između zida i plafona :)) Ovo je jedna robotska bruka za molera!

Ako poredimo posao molera i programera moler ima niz prednosti:

1. Moleru je dovoljna osnovna škola, tako da je u proseku moler bar jedno 6 godina u prednosti (4 god. srednje + 2 god. fakulteta jer ne završe fakultet svi programeri). U početku dok je mlađi moler može da radi i 18 dana mesečno, što znači da bi imao zaradu od 3000e. Dvanaest meseci puta 3000 puta 6 godina to je 216000e, dok je za to vreme programer potrošio najmanje 20000 tokom studiranja. Znači u prvih 6 godina moler ima 236000e prednosti. Ako bi moler pametno uložio taj novac, na primer na berzi, mogao bi da se penzioniše u dvadesetim, dok programer tek kreće sa svojom karijerom.

2. Za razliku od programera, moler ne mora da stažira mesecima i radi besplatno. Preduzimljiv moler može da nađe neku IT firmu i raspita se da li ta firma ima programere koji stažiraju/volontiraju ili ode do fakulteta i potraži studente. Pošto ti ljudi moraju da žive od nečega za vreme stažiranja/studiranja/volontiranja, moler bi mogao da ih angažuje za recimo 500e mesečno, što je beskonačno više od onoga koliko su u startu plaćeni. Neka mu programer zaradi 1500e, moler ima dodatnih 1000e od programera.

3. Moler stalno radi vežbe istezanja što je odlično za formu i zdravlje. Programer sedi za računarom, krivi kičmu, goji se i uništava zglobove na rukama.

4. Moler upoznaje nove ljude. Programer stiče kontakte na Fejsbuku.

5. Dobija napojnice, što u novcu, što u naturi.

6. Za mastora uvek mora biti hladnog piva u frižideru.

7. Moler je premazan svim bojama (bukvalno).

8. Dođe moler kod programera da mu okreči kuću. Kaže mu, ovo je posao od dva dana i to košta 500e. "U sunce ti" - reče programer - "pa ti imaš veću satnicu nego ja kao programer". Moler: "Toliko sam i ja zarađivao dok sam radio kao programer!".

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 09:01 · pre 75 meseci #870

Dokaz Euklidovog tvrdjenja o prostim brojevima:

Pretpostavimo da ima konačno mnogo prostih brojeva.
Neka su p1, p2, ..., pk svi ti prosti brojevi.
Neka je p = p1 * p2 * ... * pk + 1.
Po pretpostavci p je složen jer je veći od svih brojeva pm, m = 1, ..., k.
To znači da se p može prikazati kao proizvod prostih brojev.
Pošto su po pretpostavci p1, p2, ..., pk svi prosti brojevi
onda je p deljiv sa nekim od p1, p2, ..., pk.

To je kontradikcija jer p deljenjem sa bilo kojim brojm p1, p2, ..., pk
daje ostatak 1.
Zaključak da je pretpostavka o konačno mnogo prostih brojeva netačna
pa sledi da prostih brojeva ima beskonačno mnogo.

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 09:04 · pre 75 meseci #871

Citat:

BuzzLightyear

Jel ja treba da iznesem sve stvari da bi on mogao da kreči?

Nisi čuo za rekurziju?

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 09:07 · pre 75 meseci #872

Rekurzija je ono kad funkcija poziva samu sebe. Kako mogu da se iznesu stvari pomoću rekurzije?

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 09:31 · pre 75 meseci #873

Citat:

BuzzLightyear

Kako mogu da se iznesu stvari pomoću rekurzije?

Rekurzija je progamerski koncept i ne može da iznosi stvari.
Ali programirana mašina može da postupa po rekurzivnoj proceduri.

Code:
struct zid{
    x: real;
    y: real;
    z: real;
    width: real;
    height: real;
    angle: real;
    color: object;
    pattern: object;
    okrečen: boolean;
    parent: ptr;
    child: ptr;
}
function kreči(zid)
{
    if( zid.child ){
        kreči(zid.child);
    } else {
        dostuff(zid);
    }
}

Šta da radi ako zapne za neku stvar u sobi?
Iznese sve stvari iz sobe i problem svede na nulti slučaj.
Još bolje: pre krečenja pozoveš rekurzivnu proceduru koja iznosi stvari iz svih soba.

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 10:06 · pre 75 meseci #874

Moler može da hoda po nameštaju, ne mora da ga iznosi. Neke stvari moraš da rastaviš da bi ih izneo jer sastavljene ne mogu da prođu kroz vrata. Osim toga, tvoja funkcija ne bi radila kod hipotetičkih bogataša koji imaju beskonačno mnogo stvari. Pre nego što bi sve iznela preplavila bi stek, jer je količina RAM memorije konačna. Ako misliš da moler ima isti problem u slučaju bogataša sa beskonačno mnogo stvari, grešiš! Moler ne iznosi stvari, za molera je bitno jedino da je površina zidova konačna.

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 11:47 · pre 75 meseci #875

@Nedeljko, hvala, pogledacu. Na prvi pogled mi deluje da je to samo deo onog sto je Branimir rekao. Ali pogledacu detaljnije kad budem u prilici da se lepo koncentrisem :)

Potpis

Nebojsa Milanovic:
-Trumpa smatram vrhunskim predsednikom i voleo bih da živim u državi na čijem je on čelu
-Rusija ne laže, ne vodi osvajačke ratove
-Trump je svetla tačka u USA blatu
-Elon Musk, možda najpametniji i najtrezveniji Amerikanac

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 12:24 · pre 75 meseci #876

Citat:

Nedeljko
No, ne moramo ići toliko daleko do neprihvatanja svesti drugih bića. Uvođenje razumnih pretpostavki je sasvim racionalno. Ni nauka, koja počiva na sumnji, ne može bez aksioma.

Moje laicko razumevanje filozofije razume solipsizam kao nemogucnost provere da li druge svesti postoje. To ne znaci da druge svesti ne postoje niti da ih treba odbaciti.

Mislim da to nije nesto sto bi ogromnu vecinu uopste zanimalo, empirijsko prihvatanje svesnosti drugih je sasvim OK. Ovo jedino postaje problem kada se pokusava pripisati ili odbaciti svest nekog objekta dizuci znacaj toga na nivo iznad verovanja/pretpostavki.

Citat:

Čuo sam da postoji bitna razlika između evolucije stanja u redukovanom, odnosno neredukovanom obliku, tako da se može proceniti kada je došlo do redukcije. Ako je došlo pre nego što sam ja pogledao, onda ga je mačka redukovala. E, sad, ja kvantnu fiziku ne znam, pa ne mogu da tvrdim.

Ako mozes da utvrdis kada je doslo do redukcije stanja i da sebe iskljucis kao moguci uzrok onda definitivno imas nesto zanimljivo.

Potpis

DigiCortex (ex. SpikeFun) - Cortical Neural Network Simulator:
http://www.digicortex.net/node/1 Videos: http://www.digicortex.net/node/17 Gallery: http://www.digicortex.net/node/25
PowerMonkey - Redyce CPU Power Waste and gain performance! - https://github.com/psyq321/PowerMonkey

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 12:27 · pre 75 meseci #877

Citat:

DottorHeat
Mašina kojom se vrši merenje može da utiče na "kolapsiranje".

Redukcija je subjektivni koncept za koji ti je potreban posmatrac.

Bez posmatraca nemas redukciju. Imas mehanizam koji predhodi redukciji (dekoherencija) ali se redukcija odvija "drugde".

Potpis

DigiCortex (ex. SpikeFun) - Cortical Neural Network Simulator:
http://www.digicortex.net/node/1 Videos: http://www.digicortex.net/node/17 Gallery: http://www.digicortex.net/node/25
PowerMonkey - Redyce CPU Power Waste and gain performance! - https://github.com/psyq321/PowerMonkey

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 15:54 · pre 75 meseci #878

Citat:

Ivan Dimkovic: Ako mozes da utvrdis kada je doslo do redukcije stanja i da sebe iskljucis kao moguci uzrok onda definitivno imas nesto zanimljivo.

Ne da se meri reme redukcije, već da se redukcijom nešto bitno menja u daljoj evoluciji, tako da opazim da je pre mog gledanja mačka nešto pokvarila. No, nemam pojma da li je to tako. Čuo sam tako, ali treba proveriti.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 18:37 · pre 75 meseci #879

Radi pojašnjenja, nešto kao kada Džems Bond utvrđuje da li je neko pre njega ulazio u prostoriju.

Zalepi jednu dlaku na vrata, tako da dlaka otpadne prilikom otvaranja vrata i onda izađe kroz prozor. Kada sledeći put uđe, on vidi da li dlaka otpada baš tad ili je pre toga već otpala. U prvom slučaju, niko u međuvremenu nije otvarao vrata, a u drugom slučaju jeste.

Dakle, Džems Bond ne može da zna kada je u međuvremenu neko otvarao vrata ako ej to slučaj, nego samo da li su vrata u međuvremenu otvarana ili nisu.

Ovde se radi o tome da redukcija utiče na dalju evoluciju stanja i da se navodno može meriti da li je redukcije već bilo ili je tek mi vršimo. Međutim, nisam siguran u to.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Re: Da li biti programer? Buducnost profesije 18.08.2020. u 18:40 · pre 75 meseci #880

Citat:

Shadowed: @Nedeljko, hvala, pogledacu. Na prvi pogled mi deluje da je to samo deo onog sto je Branimir rekao. Ali pogledacu detaljnije kad budem u prilici da se lepo koncentrisem :)

Nije dovoljno pogledati. Radi se o vrlo neočiglednim rezultatima matematičke logike, za koje mora da se ima odgovarajuće predznanje. Za tebe je olakšavajuća okolnost da si programer, pa si familijaran sa sintaksnim načinom razmišljanja. Međutim, za to je potrebno baš dobro zagrejati stolicu u smislu jednog dobrog dvosemestralnog kursa matematičke logike. Ne DMS, pa da je logika samo jedan deo, nego dva semestra samo logike.

Potpis

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Forum kao aplikacija na telefonu

Srodne teme