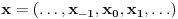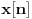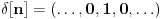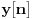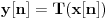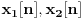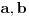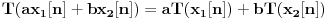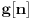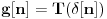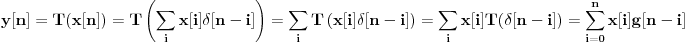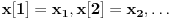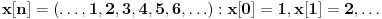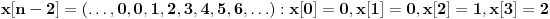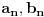Koliko vidim, tebe zanima najpre motivacija za uvođenje konvolucije, dakle zbog čega se javlja i zašto izgleda baš tako kao što izgleda a ne nekako drugačije. Pošto želiš da izbegneš analizu (integraljenje i slične stvari) primer koji ću da napišem biće iz digitalne obrade signala. Tako ćemo da preskočimo stvari koje ti nisu bliske, a i meni će biti lakše jer neću morati da opravdavam korake čije dokaze sam zaboravio. :) Takođe je dobro i to što je sva računarska obrada signala zapravo digitalna a digitalni signali su i tako razumljiviji novijim generacijama.
Počinjemo od 1d signala. Signal je uređen niz
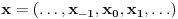
sa posebnom osobinom: za signal se uzima da je kauzalan, a to znači da su svi elementi sa indeksom manjim od nule jednaki nuli. Obično se ovaj niz označava sa
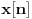
. Uzmimo za sada da su elementi niza realni brojevi. Kauzalnost je bitna odlika prirodnih signala -- to praktično znači da signal ima početak. WAV
datoteke sa snimljenim tonom su skoro savršen primer: one ne sadrže ništa drugo nego niz brojeva. Kauzalnost ćemo da iskoristimo kasnije kod konvolucije.
Jedan poseban signal se zove impuls i ima ovakav oblik:
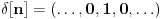
(jedinica je na nultom indeksu.)
Zatim uvodimo pojam sistema. Sistem je funkcija sa nekim posebnim osobinama. Te posebne osobine se uglavnom dogovorno uzimaju da odgovaraju osobinama raznih uređaja, mada naravno u opštem slučaju to ne mora da bude tako. Nas dalje zanimaju samo linearni i vremenski nepromenljivi sistemi. Običan tranzistorski radio je primer jedne takve naprave.
Ukratko, ubaciš ovaj niz odozgo, sa tim nulama i dobiješ drugi niz,
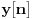
, koji se zove odziv. Ono što je sistem uradio s njim zovemo transformacija i beležimo ovako, na primer:
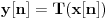
. Linearnost T se ogleda u sledećem: ako su data dva signala
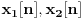
, onda za proizvoljna dva broja
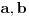
važi:
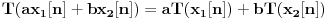
Ova osobina zove se linearnost, otud ime linearni sistem. Sistem je vremenski nepromenljiv ako je oblik odziva uvek isti do na vremenski pomeraj:
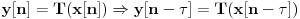
Dakle, ako signal zakasni za neko vreme
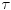
, i odziv će da zakasni za isto toliko. Ove dve osobine koristimo kako bismo videli da se svaki signal može rastaviti na zbir zakašnjenih impulsa različite veličine:
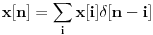
Nacrtaj sliku i biće, nadam se, jasnije. Vrednost signala u svakoj tački i zamenimo sa jednim impulsom koji je tako pomeren da ona jedinica iz njegovog pika nastupi u tački i. Pošto je visina impulsa 1, moramo da pomnožimo sa
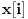
kako bismo dobili stubić visine
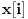
. Zatim saberemo sve stubiće i to nam tačno
daje polazni signal.
Interesantno je da, ako znamo kakav je odziv sistema na jedan impuls, to pomaže da izračunamo odziv na bilo koji drugi složeni signal (zato što smo pokazali gore da svaki složeni signal može da se razloži na impulse). Odziv na impuls zove se Grinova (Green) funkcija ili impulsni odziv. Obično se beleži sa
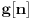
.
Neka je
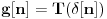
. Tada imamo sledeći izraz, koji u više navrata koristi gorepomenute osobine linearnosti i vremenske nepromenljivosti:
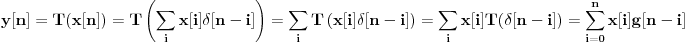
Lin. i vrem. nepromenljivost smo iskoristili da T prošetamo kroz ceo izraz, dok nije preobratio svaki impuls u odgovarajući impulsni odziv. Ono što nam je ostalo je upravo konvolucija (diskretna) dve funkcije: ulaznog signala i impulsnog odziva sistema. Na kraju smo iskoristili kauzalnost da ograničimo sumu. Ako pogledaš šta je po suštini konvolucija u nekoj tački n: to je zbir svih ehoa impulsnih odziva koje su proizveli prethodni impulsi u signalu.
f
[
Ovu poruku je menjao filmil dana 07.07.2004. u 00:27 GMT]




 Konvolucija funkcija?
Konvolucija funkcija? Re: Konvolucija funkcija?
Re: Konvolucija funkcija?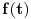
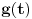


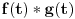
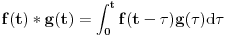
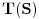
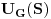

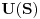
 Re: Konvolucija funkcija?
Re: Konvolucija funkcija? Re: Konvolucija funkcija?
Re: Konvolucija funkcija? Re: Konvolucija funkcija?
Re: Konvolucija funkcija? Re: Konvolucija funkcija?
Re: Konvolucija funkcija? Re: Konvolucija funkcija?
Re: Konvolucija funkcija?