Neverovatno!
Ja sam bio ubeđen da sam sinoć postavio postupak, a sad ga ne vidim. Ništa, postaviću opet.
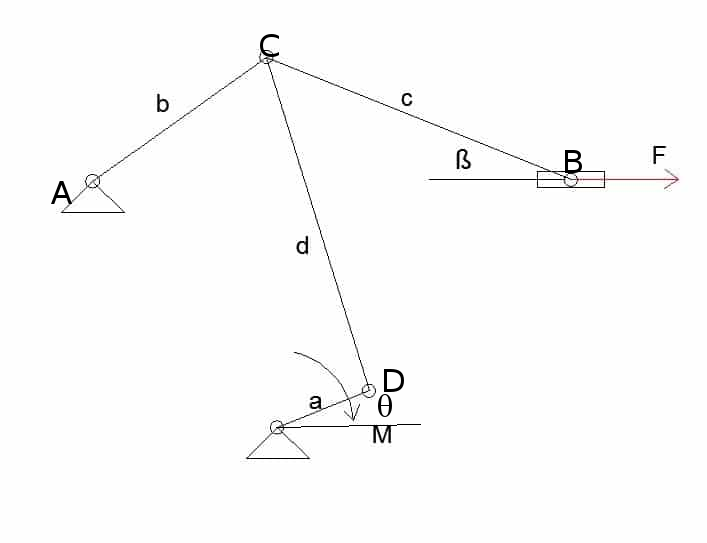
Dakle, tačke

i

su nepokretne, dužine
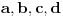
konstantne i

koordinata tačke

je konstantna. Obeležavaću je sa
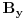
i slično za ostale taćke.
U prvom koraku na osnovu ugla

određujemo koordinate svih tačaka, kao i ugao
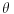
.
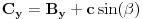
,
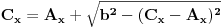
,
Tačka

se određuje kao presek krugova
(1)
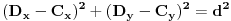
,
(2)
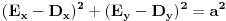
,
Oduzimanjem ove dve jednačine se dobija linearna algebarska jednačina po
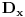
i
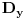
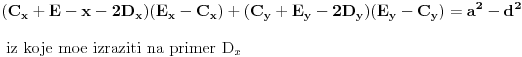
preko
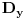
.
(3)
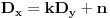
,
(4)
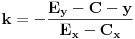
,
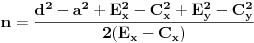
.
Zatim to zamenimo u jednačini (1)
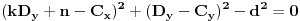
.
Ovo je kvadratna jednačina po
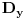
.
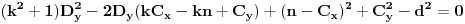
.
Odavde se može izračunati
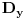
.

.
Potom pomoću (3) možemo izračunati
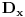
. Napokon,
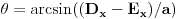
.
Sada treba izračunati diferencijale tačaka, odnosno njihove izvode po
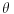
.
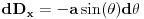
,
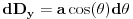
.
Takođe je
(5)
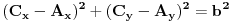
.
Diferencijali jednačina (1) i (5) daju dve linearne jednačine po
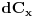
i
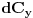
.
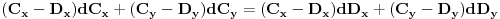
,
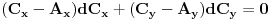
.
Rešavanjem ovog sistema dobijaju se
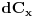
i
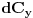
preko
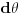
, odnosno odgovarajući izvodi po
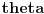
. Diferenciranjem jednačine
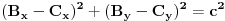
dobijamo da je
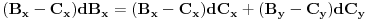
,
odnosno
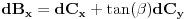
.
Napokon smo odredili izvod od
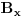
po
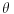
.
Sada na osnovu odnosa pređenih puteva možemo odrediti odnos sila i konačno željenu silu.
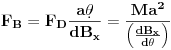
.
 [Ovu poruku je menjao Nedeljko dana 23.02.2017. u 16:17 GMT+1]
[Ovu poruku je menjao Nedeljko dana 23.02.2017. u 16:17 GMT+1]
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
