Nikakve posebne teoreme ne trebaju.
Između takvih modela je izomorfizam isto što i bijekcija, jer se interpretacija binarnog relacijskog znaka svodi na jednakost, a jednakost i različitost su bijekcijom očuvani.
Izomorfni modeli zadovoljavaju iste rečenice, ako je to neka teorema. Mislim, ima dokaz indukcijom po složenosti formule, ali se mora malo preformlisati tako da se odnosi na sve formule, a ne samo rečenice. Koristi se prelaz od valuacije jednog modela na valuaciju drugog modela preko te bijekcije. Naravno, treba prvo dokazati odnos između vrednosti termova pri valuacijama u odnosu na tu bijekciju. U ovom slučaju su jedini termi promenljive.
Neka imamo dva modela istog jezika
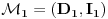
i
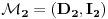
, gde su
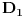
i
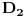
domeni, a
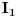
i
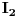
interpretacije simbola jezika i neka je
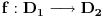
izomorfizam. Neka je
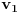
valuacija nad prvim domenom i
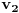
valuacija nad drugim domenom definisana sa
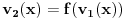
.
Za vrednosti termova pri valuacijama važi:
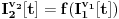
.
Dokaz:
Za promenljive važi
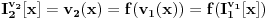
.
Prvi prelaz je na osnovu definicije vrednosti terma, drugi na osnovu definicije valuacije
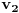
i treći na osnovu definicije vrednosti terma.
na osnovu izbora valuacije
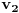
.
Za simbole konstanti je
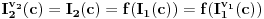
.
Prvi prelaz je po definiciji vrednosti terma, drugi po definiciji izomorfizma i treći po definiciji vrednosti terma.
Za operacijske simbole je
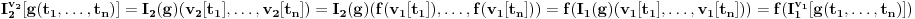
Prvi prelaz je na osnovu definicije vrednosti terma, drugi na osnovu induktivne pretpostavke da tvrđenje važi za jednostavnije terme, treći na osnovu definicije izomorfizma i četvrti na osnovu definicije vrednosti terma.
Za formule važi:

.
Dokaz:
Jednakost:
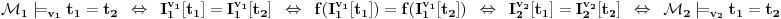
.
Prvi prelaz je na osnovu definicije relacije zadovoljenja, drugi na osnovu injektivnosti izomorfizma, treći na osnovu prethodnoog stava i četvrti na osnovu definicije relacije zadovoljenja.
Relacijske formule
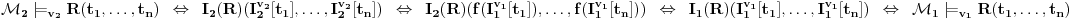
.
Prvi prelaz je po definiciji relacije zadovoljenja, drugi po definiciji valuacije
, treći po definiciji izomorfizma i četvrti po definiciji relacije zadovoljenja.
Negacija:

.
Prvi prelaz je po definiciji relacije zadovoljenja, drugi po induktivnoj pretpostavci da tvrđenje važi na jednostavnijim formulama, treći po definiciji relacije zadovoljenja.
Konjunkcija:

.
Prvi prelaz je po definiciji relacije zadovoljenja, drugi po induktivnoj pretpostavci da tvrđenje važi na prostijim formulama i treći po definiciji relacije zadovoljenja. Naravno, korišćena je konjunkcija i na metanivou.
Sa ostalim veznicima se postupa slično.
Univerzalni kvantifikator:
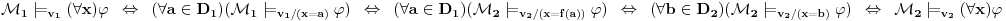
.
Prvi prelaz je na osnovu definicije relacije zadovoljenja, drugi po induktivnoj pretpostavci da tvđenje važi na jednostavnijim formulama i po definiciji prelaza sa valuacije nad
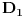
na valuaciju nad
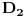
, treći po surjektivnosti izomorfizma i četvrti po definiciji relacije zadovoljenja. Naravno, koristi se univerzalna kvantifikacija na metanivou, a
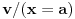
označava valuaciju
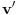
takvu da je
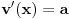
i
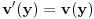
za sve promenljive

koje nisu promenljiva

.
Istinitosna vrednost formule u modelu ista za sve valuacije koje na isti način slikaju slobodne promenljive. To se takođe dokazuje indukcijom po složenosti formule, a najpre za vrednosti termova i tehnika je slična kao malopre. Odatle slei da istinitosna vrednost rečenica ne zavisi od valuacije, pa je

.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.