[es] - Koliki je broj PI

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.ptt.rs.

+2801 Profil

^{16.06.2014. u 06:21 - pre 132 meseci}

Da, kod 32-bitne verzije je postojao problem. Ispravljeno u izvornom kodu, kao i u binarnoj verziji za Windows. GNU/Linux verzija je 64-bitna.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

ms.srki
nigde
nigde

Član broj: 311977
Poruke: 12
176.104.110.*

+1 Profil

Re: Koliki je broj PI

^{16.06.2014. u 14:47 - pre 132 meseci}

broj

je dobijen eksperimentom ( pogledajte istoriju matematike , mislim da su to uradili italijani u 19 veku ) , zamena za pravilni mnogougao upisan u krugu.
trougao , 360^o:3=120^o , dužina jedne stranice 2sin

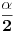
, 2sin

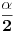
x3=1.732...x3=5.196... , 5.196...:2=2.598( za prečnik kruga)
četvorougao ,360^o:4=90^o , 2sin

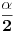
x4=1.414...x4=5.656... , 5.656...:2=2.828( za prečnik kruga)
petougao , 360^o:5=72^o , 2sin

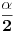
x5=1.175...x5=5.877... , 5877...:2=2.938( za prečnik kruga )
šestougao , 360^o:6=60^o , 2sin

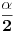
x6=1x6=6 , 6:2=3 ( za prečnik kruga ) kada kažemo

=3 , umesto kruga koristimo pravilni šestougao
sedmougao , 360^o:7=51.428...^o , 2sin

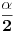
x7=0.867...x7=6.074... , 6.074:2=3.037...
osmougao , 360^o:8=45^o , 2sin

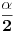
x8=0.765...x8=6.122... , 6.122:2=3.061...( za prečnik kruga)
devetougao , 360^o:9=40^o , 2sin

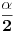
x9=0.694...x9=6.156... , 6.156:2=3.078...(za prečnik kruga)
desetougao , 360^o:10=36^o , 2sin

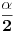
x10=0.618...x10=6.180... , 6.180...:2=3.090...(za prečnik kruga)
jedanaestougao , 360^o:11=32.727...^o , 2sin

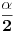
x11=0.563...x11=6.198... , 6.198...:2=3.099 ( za prečnik kruga )
dvanestougao , 360^o:12=30^o , 2sin

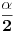
x12=0.517...x12=6.211... , 6.211...:2=3.105...( za prečnik kruga ) kada kažemo

=3.1 , umesto kruga koristimo pravilni dvanestougao
trinestougao , 360^o:13=27.692...^o , 2sin

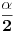
x13=0.478...x13=6.222... , 6.222:2=3.111...(za prečnik kruga)
četrnaestougao , 360^o:14=25.714...^o , 2sin

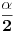
x14=0.445...x14=6.230... , 6.230...:2=3.115 ( za prečnik kruga )
petnaestougao , 360^o:15=24^o , 2sin

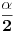
x15=0.415...x15=6.237... , 6.237...:2=3.118...(za prečnik kruga )
...
šesdesetougao , 360^o:60=6^o , 2sin

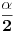
x60=0.104...x60=6.280... , 6.280...:2=3.140... (za prečnik kruga ) kada kažemo

=3.14 , umesto kruga koristimo pravilni šesdesetougao
...

Odgovor na temu

hotchimney

Član broj: 300237
Poruke: 462

+822 Profil

Re: Koliki je broj PI

^{16.06.2014. u 16:03 - pre 132 meseci}

Vrednost od 3.14.. se pripisuje Arhimedu putem konstrukcije 96-ostranog pravilnog poligona:

Citat:

Archimedes computed upper and lower bounds of π by drawing a regular hexagon inside and outside a circle, and successively doubling the number of sides until he reached a 96-sided regular polygon. By calculating the perimeters of these polygons, he proved that 223/71 < π < 22/7 (3.1408 < π < 3.1429).

U istom dokumentu se pominju i piramide u sličnom kontekstu ali nema dokaza da su Egipćani tada shvatali pojam broja π.

Odgovor na temu

Llort

Član broj: 323364
Poruke: 9

+4 Profil

Re: Koliki je broj PI

^{16.06.2014. u 20:37 - pre 132 meseci}

Citat:

Nedeljko:
Da, kod 32-bitne verzije je postojao problem. Ispravljeno u izvornom kodu, kao i u binarnoj verziji za Windows. GNU/Linux verzija je 64-bitna.

meni ne radi

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Koliki je broj PI

^{17.06.2014. u 00:48 - pre 132 meseci}

A šta se dešava?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.ptt.rs.

+2801 Profil

Re: Koliki je broj PI

^{17.06.2014. u 01:28 - pre 132 meseci}

Broj pi su drevne civilizacije određivale merenjem, a Arhimed čistim računom bez merenja.

Prvo je trebalo da bude jasno da ako je R prečnik kruga, r njegov poluprečnik, P površina, a O obim, da je

(*) O/R = P/r²,

tj. da se u oba obrasca pojavljuje identična konstanta. Starim Grcima je to bilo jasno jer se npr. krug može podeliti na n jednakih isečaka, od kojih se može formirati figura približno jednaka pravougaoniku (utoliko više ukoliko je n veće), čije su ivice poluprečnik i poluobim. Odatle je

P=rO/2,

odakle se i iz R=2r lako dobija jednakost (*).

Obim upisanog pravilnog n-tougla u krug je manji od obima kruga, jer je tetiva nad kružnim lukom kraća od samog luka, budući da je duž najkraći put između dve tačke. Taj obim iznosi 2r*n*sin(pi/n), pa je

n*sin(pi/n)<pi

Sa druge strane je površina opisanog pravilnog n-tougla oko kruga veća od površine tog kruga jer poligon obuhvata krug. Ta površina iznosi n*r²*tan(pi/n), pa je

pi<n*tan(pi/n).

Neka je c(x)=2*cos(x), s(x)=2*sin(x). Iz formule za sinus i kosinus polovine ugla zaključujemo da je

.

Dakle,

.

Na kraju je

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Llort

Član broj: 323364
Poruke: 9

+4 Profil

Re: Koliki je broj PI

^{17.06.2014. u 10:25 - pre 132 meseci}

Citat:

Nedeljko:
A šta se dešava?

nista....

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.ptt.rs.

+2801 Profil

Re: Koliki je broj PI

^{17.06.2014. u 13:47 - pre 132 meseci}

Arhimed je imao sijaset rezultata o površinama i zapreminama iz kojih je znao da se ista konstanta pojavljuje i u obrascima za površinu i zapreminu lopte. Postoji Arhimedov rad "o merenju kruga", gde je baš ovako računao broj pi. Ne pojavljuju se trigonometrijske funkcije. Isti račun je izložen u savremenom obliku. Međutim, navedene formule o trigonometrijskim funkcijama polovine ugla imaju geometrijsku interpretaciju, koja mu je već bila poznata. Što se kvadratnog korena tiče, naravno da u svakoj iteraciji trebaju samo donje aproksimacije. Osim toga, znalo se za specijalan slučaj Njutnovog metoda tangente za računanje kvadratnog korena.

Citat:

Llort: nista....

Koji OS koristiš? Pretpostavljam Windows 7. Celu 7z arhivu treba da raspakuješ u neki folder. Zatim klikni na exe fajl i onda pritisni ENTER ili RETURN, kako li ti već piše na tastaturi. Šta se onda dešava? Ne pojavljuje se ništa?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

B3R1
Berislav Todorovic
NL

Član broj: 224915
Poruke: 853

+681 Profil

Re: Koliki je broj PI

^{17.06.2014. u 15:20 - pre 132 meseci}

Arhimedova aproksimacija (3+1/7) je zvanicno koriscena sve do XVI veka, kada je holandski matematicar Ludolph van Ceulen izracunao pi na 35 decimala (zato se pi i zove ponekad Ludolfov broj) i taj svoj rezultat opisao u knjizi "O krugu i kamati" (Vanden circkel ende interest", Leiden 1615): http://books.google.nl/books?id=G4c_AAAAcAAJ. Inace, u toj knjizici mozete da vidite da je u to vreme vec postojao simbol korena, racionalni brojevi su se pisali kao razlomci, jer decimale nisu postojale (umesto 3.14159 on je pisao 3 14159/100000), trigonometrijske funkcije "sinuum, tangentium, secantium" su bile definisane, doduse tabelarno itd. Deo o kamati je verovatno ubacen po narudzbini nekog mecene-zelenasa, jer je neko morao da plati stampanje knjige ... :-)

Odgovor na temu