[es] - Euklidov peti postulat.

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu.

+64 Profil

^{07.11.2004. u 08:11 - pre 249 meseci}

Evo, pre nego što mr. Nedeljko da pravi odgovor, da probam ja, iz jutarnje smene.

Kratki odgovor na tvoje pitanje je: peti postulat je aksioma.

Malo da razmotrimo kako to uopšte nastaju teorije, aksiome i tsl. Bilo bi nam mnogo lakše da je npr. bog u svojim zapovestima naveo i potrebne matematičke aksiome. Ali, taj posao je prepušten nama i mi ga otprilike izvodimo na sledeći način.

Kada se nakupi dovoljno intuitivnog materijala, pokušavamo da izvučemo srž tako što izbacujemo stvari koje su posledica, podižemo nivo apstrakcije i proveravamo da ne postoji kontradikcija.

Ono što ostane su "aksiome", tj. početna pravila koja su nepohodna da bi sve funkcionisalo onako kako želimo; ali koja ne možemo (ne želimo) dovoditi u pitanje, jer smo došli do granice razumevanja. Kao što ti kažeš, "zašto da dokazujem ono što je očigledno". Dakle, matematičari se "prave ludi" i kažu da moraš da dokažeš i ono što je očigledno, ako to nije aksioma, a za aksiome (iako su i one "očigledne") to ne zahtevaju.

Kao što geometrija nije aritmetika iako ih analitička geometrija spaja, tako su i aksiome geometrije nešto sasvim drugo od aksioma aritmetike. Dakle, postoji intuitivno shvatanje da su neke stvari različite i one se u krajnjem ishodu prepoznaju u različitim teorijama. Zato imamo osnova da kažemo da neki skup aksioma generiše teoriju koju na kraju prepoznajemo kao npr. geometriju.
Kao što vidiš, ovde su se sada stvari obrnule: aksiome su derivat intuicije, ali kada ih postavimo, one generišu intuiciju.

E, sad, zašto sam ja sve ovo napričao, bog da me ubije (znam samo da sam dva puta pomenuo boga (sad tri puta) bez nekog posebnog razloga, pa će neko pomisliti da je ovo religijska rasprava :)
...

Zahtev je da su aksiome međusobno nezavisne, tj. da nijednu od njih ne možemo izvesti oz ostalih. Peti postulat je "čudan" jer je neobično glomazan, pa su vekovima ljudi pokušavali da ga izvedu iz ostalih postulata. Ali to nije moguće, a dokaz za to je da ako umesto petog postulata ubacimo njegovu negaciju, to sa ostalim aksiomama čini neprotivrečnu teoriju (geometrija Lobačevskog).

Logički rečeno, pitanje kako ne može da se dokaže peti postulat je isto kao da pitaš kako ne može da se dokaže bilo koja aksioma geometrije. Ne verujem da si se ikada pitao zašto ne može da se dokaže da za svake dve tačke postoji jedinstvena prava koja ih sadrži...

Napisa' ja svašta, pa ko pročita, svaka mu ...

Odgovor na temu

srki
Srdjan Mitrovic
Auckland, N.Z.

Član broj: 2237
Poruke: 3654
..chandran.sbs.auckland.ac.nz.

+3 Profil

Re: Euklidov peti postulat.

^{07.11.2004. u 09:08 - pre 249 meseci}

U, bre, bas si se raspisao :-)
Dovoljno je bila samo tvoja druga recenica da shvatim o cemu se radi:

Citat:

Kratki odgovor na tvoje pitanje je: peti postulat je aksioma.

Nego kada sam za taj peti postulat prvi put cuo to je bilo u prvom razredu srednje skole i nisam se secao da je profesor pominjao da je to bila aksioma i zato mi nije bilo jasno kako ne moze da se dokaze jer je meni na prvi pogled izgledalo da je stvar jednostavno dokaziva. Ali sada znam da bi taj dokaz kada bi se razlozio na najsitnije detalje u stvari samo koristio tu aksiomu. Nisam proveravao ali to je jedino objasnjivo shvatanje.

Citat:

Logički rečeno, pitanje kako ne može da se dokaže peti postulat je isto kao da pitaš kako ne može da se dokaže bilo koja aksioma geometrije. Ne verujem da si se ikada pitao zašto ne može da se dokaže da za svake dve tačke postoji jedinstvena prava koja ih sadrži...

Ma naravno. Cela zabuna je bila u tome da nisam znao da je to aksioma.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.vdial.verat.net.

+2801 Profil

Re: Euklidov peti postulat.

^{07.11.2004. u 10:08 - pre 249 meseci}

Nemam pojma na kojeg mr. Nedeljka mislite. Ja sam jednostavno Nedeljko Stefanović ako je slučajno reč o meni. Što se tiče petog Euklidovog postulata, on jeste bio aksioma kod Euklida. Zapravo, ono što bismo mi danas nazivali aksiomama on je podelio u dve grupe: grupu aksioma (bilo ih je devet) i grupu postulata (ukupno pet). Takođe, kod njega reč "definicija" označava sasvim drugi pojam nego danas kod nas.

Dokazivanje elementarnih stavova ima smisla samo ako se zna od čega se polazi. Na primer: zadatak dokazivanja da za svaki pozitivan realan broj

važi

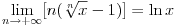
ima smisla samo ako se zna koja je definicija logaritma izabrana. Recimo, pomenuti limes može biti definicija prirodnog logaritma. Tada nema smisla dokazivati pomenutu relaciju, ali ima smisla dokazivati da je prirodni logaritam inverzna funkcija eksponencijalnoj. Sa druge strane, ako se prirodni logaritam definiše kao inverzna funkcija eksponencijalnoj, onda ima smisla dokazivati gore navedenu relaciju.

Još bolji primer su aksioma supremuma i Dedekindova aksioma kod aksiomatizacije uređenog polja realnih brojeva. Koju god od njih da uvrstimo u spisak aksioma, ona druga (uz ostale algebarske aksiome) postaje teorema. Koju ćemo od njih izabrati za aksiomu, to je stvar našeg izbora.

Međutim, to što je nešto aksioma i dalje ne znači da ne možemo ispitivati da li je toj aksiomi zaista mesto u spisku aksioma, to jest da li se može izvesti iz drugih aksioma. Postoje sistemi aksioma koji nisu nezavisni (minimalni), to jest oni kod kojih kada izbacimo neku aksiomu iz spiska aksioma, ona i dalje ostaje teorema. Recimo, uz aksiome uređenog polja ne bi imalo potrebe uvoditi i aksiomu supremuma i Dedekindovu aksiomu kao aksiome. Dovoljno je uvesti jednu od njih, a onda je ona druga teorema.

Upravo je to mučilo ljude u vezi sa petim Euklidovim postulatom: može li se on izvesti iz ostalih Euklidovih aksioma i postulata kao teorema? Ispostavilo se da on ne zavisi od ostalih Euklidovih aksioma i postulata. Naime, postoje modeli u kojima važe sve Euklidove aksiome i posulati (modeli Euklidske Geometrije), kao i modeli u kojima važe sve Euklidove aksiome i postulati izuzev petog postulata i pri čemu u tim modelima važi njegova negacija (modeli Geometrije Lobačevskog).

Najzad, peti Euklidov postulat već više od sto godina nije niti aksioma niti postulat jer Euklidova aksiomatizacija Geometrije nije više u upotrebi. Postoje drugi aksiomatski sistemi u kojima se sve to daleko preciznije izlaže. Na primer, Dragomir Lopandić i Zoran Lučić su u svojim udžbenicima Geometrije koristili aksiomatiku Borsuka i Šmileve. U toj aksiomatizaciji se kao aksioma paralelnosti Euklidske Geometrije koristi Plejferova aksioma i u njoj je peti Euklidov postulat teorema.

Inače, postoje veoma važne matematičke teorije kao što je Cermelo-Frankelova aksiomatska Teorija Skupova ZFC kod kojih se zna da im aksiome nisu nezavisne, ali to nikome ne smeta. Zahtev da aksiomatika bude nezavisna nije obavezan u Matematici, mada kada nije jasno da li neka aksioma sledi iz preostalih aksioma neke teorije, matematičari nemaju mira dok to ne razreše. U istoriji Algebre se zna za takve važne primere.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
*.dial.InfoSky.Net.

Profil

Re: Euklidov peti postulat.

^{07.11.2004. u 17:13 - pre 249 meseci}

Nadovezao bih se na Nedeljkovo razmatraje, uz prethodni pozdrav. Dokazivanje 5. postulata podrazumeva dokazivanje 5. postulata iz ostalih postulata iaxioma, te, eventualno, teorema izvedenih iz tih preostalih postulata & axioma. U Lučićevom udžbeniku (mislim da se glava zove "Istorijat dokazivanja 5. postulata", mada je možda sledeća parafraza iz "Ležandrovih teorema") piše da, ukolko negiramo 5. postulat, dobijamo geometriju u kojoj se 2 prave mogu beskonačno približavati, a da se ipak ne seku. Ovo je dalje equivalentno sa tvrđenjem da skup tačaka koje su podjednako udaljene od jedne fixne prave u poluravni, kojoj je ta prava rub nije prava. Pošto je "očigledno" da to nije istina, Ležandr zaključuje da 5. postulat jeste dokaziv iz ostalih axioma. Međutim to nije baš tako. Naime ukoliko zamenimo 5. postulat (ili neki od nj equivalenata) sopstvenom negacijom, dobijamo novu geometriju - Hiperboličku geometriju, različitu od one "očigledne" Euklidovske geometrije.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu.

+64 Profil

Re: Euklidov peti postulat.

^{08.11.2004. u 13:38 - pre 249 meseci}

Citat:

Međutim, to što je nešto aksioma i dalje ne znači da ne možemo ispitivati da li je toj aksiomi zaista mesto u spisku aksioma, to jest da li se može izvesti iz drugih aksioma.

Baš o tome pričah. Dakle, kandidata za aksiomu odbacujemo iz sistema ako se pokaže da se može izvesti iz ostalih. Ono za šta se pokaže da nije neophodno, ne zovemo aksiomom. I upravo način na koji su to Lobačevski (i Boljaji) uradili, nezavisnost dokazujemo ispitivanjem protivrečnosti sistema sa negacijom ispitivanog kandidata.

Ne bih baš delio aksiome na one kojima jeste mesto i one kojima nije mesto u sistemu. Jednostavno, nešto ili jeste ili nije aksioma, a pre utvrđivanja možemo taj iskaz zvati "kandidat". U stvari ova tema je veoma interesantna. Mi zaista za mnoge stvari kažemo da je aksioma, kao što je Nedeljko naveo primer sa aksiomom supremuma/Dedekindova. Ali nikad ne bi rekli da su obe aksiome neke teorije. Stavljajući jednu ili drugu, dobijamo "istu" teoriju. Još je interesantniji slučaj sa iskazima koji nisu ekvivalentni ili su čak suprotni. Zašto kažemo da je ono što je uradio Lobačevski "geometrija" iako je suprotna intuiciji?

Kada sam rekao da je peti postulat aksioma upravo sam mislio na to da postoji njena intuitivna zamena u savremenom sistemu. Kada se zameni nečim intuitivno različitim onda to više nije Euklidova geometrija, kako se i danas naziva standardna geometrija, već nešto drugo.

Odgovor na temu