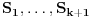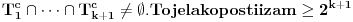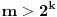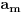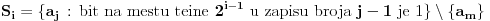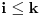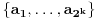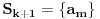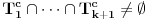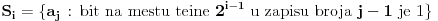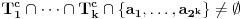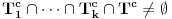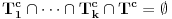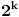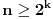Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.

Zadatak sa olimpijade, da li je tačan ili ja grešim?

[es] :: Matematika :: Zadatak sa olimpijade, da li je tačan ili ja grešim?

[ Pregleda: 1649 | Odgovora: 1 ] > FB > Twit

Postavi temu Odgovori

Autor
Pretraga teme: Traži
Markiranje Štampanje RSS

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8752
*.3gnet.mts.telekom.rs.



+2807 Profil

icon Zadatak sa olimpijade, da li je tačan ili ja grešim?15.08.2013. u 03:53 - pre 156 meseci
Mislim da zadatak 3 prvog dana takmičenja na olimpijadi 2012 nije tačan, pa bih da me neko uputi gde grešim. U prilogu prilažem zadatke koje sam skinuo sa zvaničnog sajta međunarodnih matematičkih olimpijada.

Pretpostavimo da u nekoj fazi igre igrač B zna da zamišljeni broj pripada nekom skupu 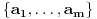, gde je 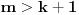i gde su svi od brojeva međusobno različiti. Na početku je to skup 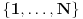. Igrač B može postaviti 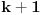pitanja u vezi sa skupovima

,
,
...
.

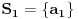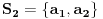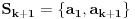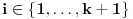
Neka je za 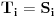ako je igrač A rekao da zamišljeni broj pripada skupu 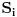, odnosno 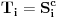ako je igrač A rekao da zamišljeni broj ne pripada skupu 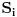. Obzirom da igrač A nije mogao da slaže svih 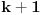puta, ne može biti 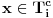za sve 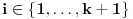, odnosno igrač B može da odbaci elemente skupa 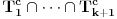. To znači da igrač B može da suzi skup mogućnosti ako je skup neprazan.

Ukoliko je zamišljeni broj jednak 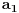, onda je 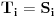za svako 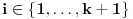, odnosno 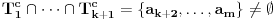. Dakle, ako dobijemo da je 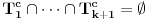, onda svakako možemo odbaciti element 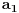kao nemoguć.

Znači, u svakom slučaju, ako je 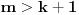, posle 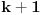postavljenih pitanja možemo suziti izbor ili odbacivanjem elemenata skupa 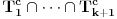ako je neprazan ili elementa 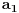ako je .

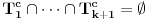Kada se skup mogućnosti svede na skup sa ne više od 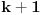elemenata, ako je 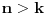, onda igrač B može da se opredeli baš za taj skup i zamišljeni broj će mu svakako pripasti, pa igrač B može da garantuje pobedu kad god je .

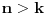No, u tom slučaju tvrđenje pod 2 koje treba dokazati nije tačno.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Prikačeni fajlovi
2012_srp.pdf 2012_srp.pdf - 236.24k
 
Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8752
*.3gnet.mts.telekom.rs.



+2807 Profil

icon Re: Zadatak sa olimpijade, da li je tačan ili ja grešim?15.08.2013. u 08:57 - pre 156 meseci
Evo gde sam pogrešio:
Citat:
Nedeljko: Ukoliko je zamišljeni broj jednak , onda je za svako

To je slučaj da je igrač A govorio isključivo istinu. Ako je malo i lagao, onda je za takvo da je slagao na -tom pitanju.

Da napišem tačno rešenje zadatka:

Igrač B treba da postavi seriju od pitanja tako da bude , ali treba dokazati da je to moguće za . Igrač B može da pretpostavi da je zamišljeni broj jednak i da planira postavljanje pitanja

, .

Ako uvek dobije odgovor "ne", onda skup ima bar dva elementa, i tačno jedan iz skupa . Onda je lako izabrati pitanje i svakako će biti . Za odbacivanje elemenata ovog skupa nam ne treba pretpostavka da je zamišljeni broj jednak jer bar jedan od ovih odgovora mora biti tačan.

Ako li pak jednom kaže "da", recimo na -tom pitanju, onda igrač B zapamti to pitanje i taj skup za koji je pitao označi sa prekida pitanja po planiranom nizu i postavlja novi niz od pitanja znajući da je igrač A upravo slagao i da na narednih pitanja mora dati bar jedan tačan odgovor, a tada je lako postaviti pitanja



tako da bude , a samim tim i , u kom slučaju igrač B može eliminisati elemente skupa . Opet, za odbacivanje elemenata ovog skupa nam ne treba pretpostavka da je zamišljeni broj jednak jer bar jedan od ovih odgovora mora biti tačan.

Ukoliko se desi da pri ovoj strategiji ipak bude , to znači da pretpostavka da je zamišljeni broj jednak nije tačna, pa možemo njega odbaciti.

Stoga igrač B može da sužava skup mogućnosti dokle god ima više od elemenata, pa ako je , on može kada broj mogućnosti padne na ne više od da stane, da se opredeli baš za taj skup i da pobedi.

Napisaću kasnije rešenje zadatka pod 2.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
Odgovor na temu

[es] :: Matematika :: Zadatak sa olimpijade, da li je tačan ili ja grešim?

[ Pregleda: 1649 | Odgovora: 1 ] > FB > Twit

Postavi temu Odgovori

Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.