Pazi, ja ne znam PHP (mada bih verovatno znao da pročitam). Tvoje rešenje problema sa stringovima je korektno, ali nije ni izbliza efikasno kao neka druga rešenja. To gugl ne traži. Ako si do sada uneo milion reči, onda bi za milion i prvu morao da je uporediš sa svih milion koje se nalaze u listi. To znači da bi nakon unošenja n stringova broj poređenja u najgorem slučaju bio
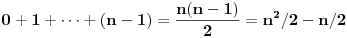
.
Ovo znači da za 10 puta više unetih reči treba 100 puta više poređenja
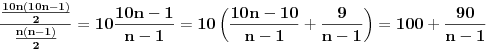
.
Kada je

veliko,
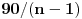
je malo (izračunaj ga kada je n jednako hiljadu, odnosno milion, odnosno 100 miliona), tako da je za 10 puta veći broj stringova broj poređenja na koje se svakako troši vreme oko 100 puta veći.
Postoji algoritam čije utrošeno vreme raste mnogo sporije. Evo, prilažem rešenje tog zadatka:
Code (cpp):
#include <string>
class StringCounter
{
struct Node
{
typedef Node *Three;
Three nextLetter[256];
unsigned int counter;
Node()
{
counter = 0;
for (int i = 0; i < 256; ++i) {
nextLetter[i] = 0;
}
}
} rootNode;
unsigned int currentMax;
std::string currentString;
public:
StringCounter()
{
currentMax = 0;
}
void insert(const std::string &str)
{
Node *currentNode = &rootNode;
size_t size = str.size();
for (size_t i = 0; i < size; ++i) {
unsigned char ch = str[i];
if (currentNode->nextLetter[ch] == 0) {
Node *nextNode = new Node;
currentNode->nextLetter[ch] = nextNode;
currentNode = nextNode;
} else {
currentNode = currentNode->nextLetter[ch];
}
}
++(currentNode->counter);
if (currentNode->counter > currentMax) {
currentMax = currentNode->counter;
currentString = str;
}
}
std::string getMaxString() const
{
return currentString;
}
};
Šta je fabula radnje? Imaš zasebnu strukturu podataka koja se zove drvo. Drvo ima čvorove od kojih svaki sadrži neke podatke (koji zavise od toga čemu drvo služi) i pokazivače prema drugim čvorovima. Pritom, da bi se to zvalo drvo, ne sme postojati ciklus tako da npr. čvor A pokazuje na čvor B, čvor B pokazuje na čvor C, a čvor C pokazuje na čvor A (odnosno da neki čvor pokaže na samoga sebe) i mora postojati tačno jedan čvor na koji ne pokazuje nijedan drugi čvor, pri čemu taj čvor zovemo korenom. Izuzetak je slučaj kada je drvo prazno, to jest nema nijedan čvor, pa ni koren. Ta situacija se dozvoljava. Ako znamo gde se nalazi koren drveta, lako možemo doći do svih ostalih čvorova drveta.
Možda će ti biti jasnije sa slike
http://en.wikipedia.org/wiki/Tree_%28data_structure%29
Tamo svaki čvor može imati najviše dva potomka, kada se drvo zove binarno, a inače ih može biti i više.
Svaki znak ima neku vrednost od 0 do 255. Koren predstavlja prazan string i grana se na 256 grana prema tome koje je prvo slovo u stringu. Neki od pokazivača su jednaki nuli, što znači da ne pokazuju ninakakav čvor. Ako bismo u prazan kontejner ubacili reč "Ana", onda bismo osim korena imali joštri čvora. Koren bi svojim pokazivačem koji odgovara slovu "A" pokazivao na jedan novi čvor, a ostali pokazivači korena bi bili nule. Taj novi čvor svojim pokazivačem koji odgovara slovu "n" pokazuje na drugi novi čvor, a ostali njegovi pokazivači su nule i na kraju taj drugi novi čvor pokazuje svojim pokazivačem koji odgovara slovu "a" na treći novi čvor.
Međutim, postavlja se pitanje šta da radimo ako se doda reč "Ananas". Onda će treći novi čvor koji se pojavio dodavanjem reči "Ana" svojim pokazivačem koji odgovara slovu "n" pokazivati na još jedan novi čvor itd. Ukupno ćemo osim korena imati još šest čvorova. Kako znati da su ubačene dve reči od kojih je jedna početni deo druge?
Svaki čvor mora da nosi informaciju da li kontejner sadrži reč koja predstavlja put od korena do tog čvora. U našem slučaju, osim te informacije nam treba i informacija koliko je reč puta ubačena, tj. brojač.
Na kraju, negde sa strane pamtimo koliko puta se pojavljuje najčešća reč i koja ej to reč, pa kada utvrdimo da se reč koju ubacujemo do tada češće pojavljivala, onda te informacije sa strane ažuriramo.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.