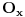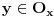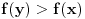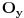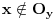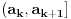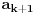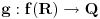Ne, nije, naravno... Nego nisam nesto stizao da kvalitetnije odgovorim. A mozda to necu uciniti ni sada :)
U svakom slucaju, ono sto se moze lako primetiti za ovakvu funkciju je sledeca osobina: ako je
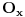
okolina tacke x u kojoj je ona lokalni minimum i ako postoji
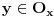
takvo da je
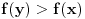
, tada postoji okolina
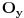
tacke y, takva da je
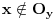
. Ovo je naravno zato sto mora postojati okolina tacke y u kojoj je ona lokalni minimum, pa takva ne moze sadrzati x, jer je vrednost funkcije u y veca.
E sad, kako ovo iskoristiti? Evo nekog pokusaja: navedena logika se dalje moze nastaviti na okolinu tacke y, itd. Time dobijamo jedan niz okolina, neka su to recimo otvoreni intervali, koji ne bi smeo da ima prazan presek. Cini mi se da u tom slucaju, tacka koja bi se dobila kao granicna vrednost niza tacaka sa navedenom osobinom, ne bi imala okolinu u kojoj je lokalni minimum funkcije f.
Ako je tako, onda znaci da smo dobili, kao presek u navedenom postupku, otvoreni interval u kome nema tacaka u kojima funkcija ima strogo vecu vrednost od tacke lokalnog minimuma, pa je znaci tu konstantna. Dalje bi se mogla koristiti ranije navedena logika...
Funkcija koja u svakoj tački dostiže lokalni minimum.
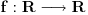u svakoj tački dostiže lokalni minimum. Dokazati da je skup njenih vrednosti najviše prebrojiv i konstruisati takvu funkciju sa beskonačnim skupom vrednosti.
