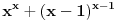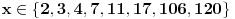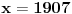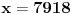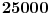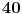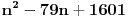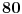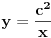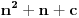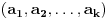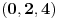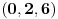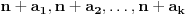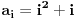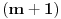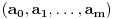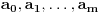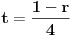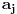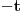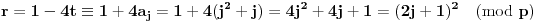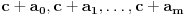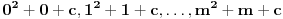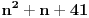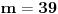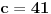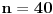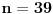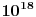Citat:
Bojan Basic:
Ali OK, ako uzimamo u obzir samo kvadratne polinome po jednoj promenljivoj takve da daju proste vrednosti za sve vrednosti argumenta od
pa do što veće gornje granice (da li sam sad dovoljno restriktivan? :)), izraz
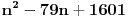
da je proste vrednosti za
u rasponu od
do
.
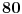
A inače, da se nadovežem na ovo. Priložiću dokaz da, ukoliko je tačna hipoteza o prostim
-torkama (a niko zaista ne sumnja u tačnost te hipoteze), tada za svaki prirodan broj
postoji prirodan broj
takav da izraz
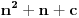
uzima proste vrednosti za sve
u rasponu od
do
!
Za početak, da vidimo šta tvrdi hipoteza o prostim
-torkama. Za
-torku nenegativnih celih brojeva
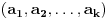
kažemo da je
prihvatljiva ukoliko ne postoji prost broj
takav da se u posmatranoj
-torci javljaju svi mogući ostaci pri deljenju sa
. (Primera radi, trojka
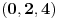
nije prihvatljiva jer sadrži sve ostatke pri deljenju sa
, dok recimo trojka
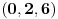
jeste prihvatljiva.) Hipoteza o prostim
-torkama tvrdi da za svaku prihvatljivu
-torku
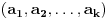
postoji beskonačno mnogo prirodnih brojeva
takvih da su sve vrednosti
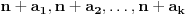
proste.
Vratimo se sada na dokaz najavljenog. Neka je dat prirodan broj
. Označimo
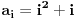
. Tvrdimo da je
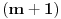
-torka
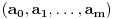
prihvatljiva. Zaista, primetimo najpre da su svi brojevi
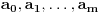
parni, pa prost broj
ne narušava prihvatljivost. Neka je sada
neparan prost broj, i pretpostavimo da on narušava prihvatljivost (tj. da se među brojevima
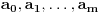
javljaju svi ostaci pri deljenju sa
). Neka je
proizvoljan kvadratni neostatak po modulu
koji pritom daje ostatak
pri deljenju sa
(kako su brojevi
i
uzajamno prosti, ovakva vrednost
može se odabrati na osnovu kineske teoreme o ostacima), i označimo
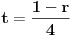
. Kako smo pretpostavili da
narušava prihvatljivost, među brojevima
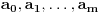
postoji neki, recimo
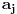
, koji je kongruentan sa
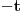
po modulu
. No, sada imamo
,
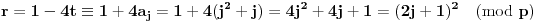
a ovo je u kontradikciji s činjenicom da je
kvadratni neostatak po modulu
.
Time smo pokazali da je
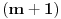
-torka
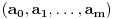
prihvatljiva. Odatle sledi da postoji prirodan broj
takav da su svi brojevi
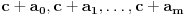
prosti. No ovi brojevi su upravo
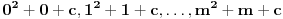
, tj. vrednosti izraza
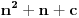
za
u rasponu od
do
. Kraj dokaza.
Polinom
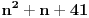
zapravo je ilustracija da za
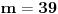
imamo
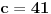
(mala ispravka, ranije smo komentarisali da posmatrani polinom uzima proste vrednosti do
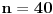
, zapravo je do
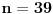
). Da vidimo za koje
izraz
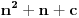
uzima proste vrednosti za
u rasponu od
do
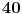
(tj. makar samo za jedan korak više od ovog što imamo). Odgovor je, nažalost, da ne znamo eksplicitno koliko
iznosi. (Gornje tvrđenje kaže da takvo
postoji — doduše kondicionalno, no korišćena pretpostavka je veoma verovatna — ali ne znamo ništa o tome koliko takvo
mora biti veliko.) Zna se da traženo
nije manje
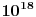
, ali verovatno je mnogo veće i od ove granice.
Ljubičice crvena, što si plava kô zelena trava.
uzastopni stepeni i prajmovi
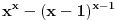
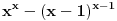, kada je x ceo pozitivan broj postoji samo 6 prostih brojeva. 
... moze da da rezultat ali najcesce je vrlo pogresan put.
i nije problem koliko se nesto smislja vec je bitnije da to bude rezultat nekog (sistematskog) rada ... barem po meni, ali mislim da nema potrebe ici dalje, svako ima pravo na svoj metod rada.
