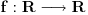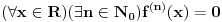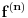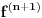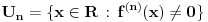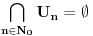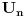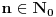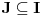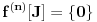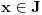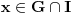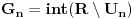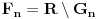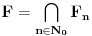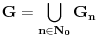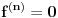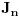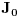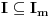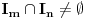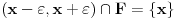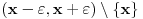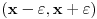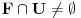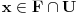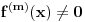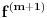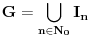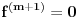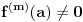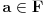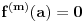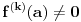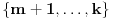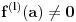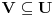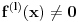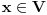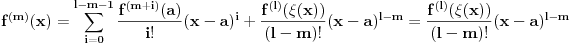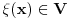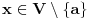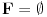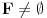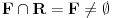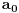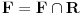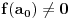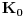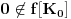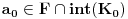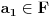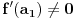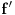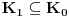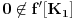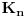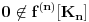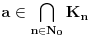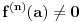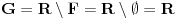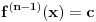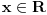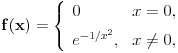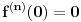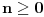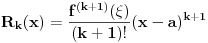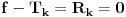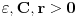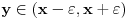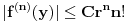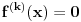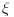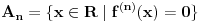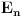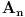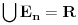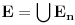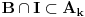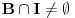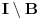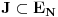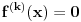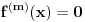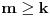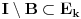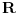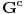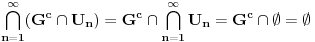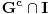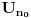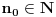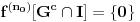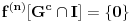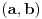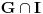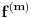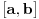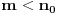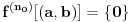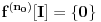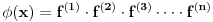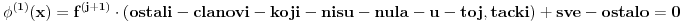Pretpostavimo suprotno, da funkcija
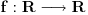
nije polinomska, ali da važi
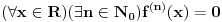
.
1 .
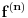
je neprekidno.
Dokaz: Neprekidno je kao diferencijabilno jer postoji
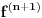
.
2. Oznaka:
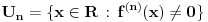
.
3. Skup

svih tačaka koje imaju okolinu na kojoj je funkcija

polinomijalna je otvoren i svuda gust i na njemu je funkcija lokalno polinomijalna.
Dokaz: Netrivijalno je dokazati da je skup

svuda gust. Obzirom da je
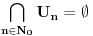
i da su skupovi
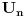
otvoreni, po Berovoj teoremi za svaki pravi interval

postoji
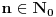
takvo da
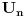
nije gust u

, odnosno postoji pravi interval
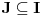
takav da je
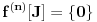
. No, to znači da je

polinomijalna na intervalu

. Za ma koje
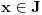
važi
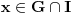
.
4. Oznaka:

je niz disjunktnih otvorenih intervala čija je unija skup

.
5. Oznaka:
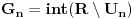
- skup tačaka koje imaju okolinu u kojoj je funkcija polinomijalna stepena manjeg od

,
6. Oznaka:
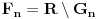
,
7. Oznaka:
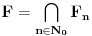
.
8. Skup

je zatvoren,
Dokaz: Na osnovu 1.
9.
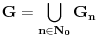
.
10. Ako je funkcija na pravom intervalu polinomijalna, taj polinom je jednoznačno određen.
Dokaz: Polinom je jednoznačno određen vrednostima u bilo kojih beskonačno mnogo tačaka.
11. Neka je

bilo koji pravi otvoreni interval na kome je funkcija

lokalno polinomijalna. Ona je na njemu polinomijalna.
Dokaz: Za ma koji kompaktan interval
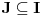
ma koja tačka
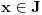
ima okolinu u kojoj je funkcija

polinomijalna. Takve okoline čine otvoreni pokrivač kompaktnog skupa

. Iz njega možemo izdvojiti konačan potpokrivač. Obzirom da je na svakom elementu konačnog potpokrivača funkcija

polinomijalna, možemo uočiti prirodan broj

koji je veći od stepena svih tih konačno mnogo polinoma, pa na kompaktu

važi
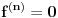
, pa je na unutrašnjosti intervala

funkcija

polinomijalna. Neka je
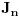
rastući niz kompaktnih podintervala od

takvih da je unija njihovih unutrašnjosti interval

. Funkcija

je polinomijalna na svakom od njih, a prema 10 su svi ti polinomi jednoznačno određeni vrednošću funkcije na
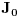
, pa se radi o jednom polinomu. Stoga je funkcija

polinomijalna na celom intervalu

.
12. Funkcija

je polinomijalna na svakom od intervala

.
Dokaz: Na osnovu 11.
13. Izvodi funkcije

bilo kog reda na bilo kom kraju intervala

jednaki su odgovarajućim izvodima na tom kraju intervala

polinoma kome je funkcija

jednaka na intervalu

.
Dokaz: Na osnovu 1.
14. Tejlorov razvoj funkcije u okolini bilo kog od krajeva intervala

je konačan i jednak funkciji

na intervalu

.
Dokaz: Sledi iz 13 i osobina polinoma.
15: Ako je funkcija

polinomijalna na dva intervala koji imaju jedan zajednički kraj, onda je polinomijalna i na uniji zatvorenja tih intervala. Opštije, ako je funkcija

lokalno polinomijalna na nekom intervalu bez nekog diskretnog skupa tačaka, onda je polinomijalna na zatvorenju tog intervala. Stoga intervala

ima beskonačno mnogo.
Dokaz: Sledi iz 14.
16: Svaki od krajeva intervala

pripada skupu

.
Dokaz: U suprotnom postoji okolina

tog kraja u kojoj je funkcija

polinomijalna, pa je
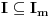
za neko

. No, u tom slučaju je
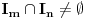
suprotno izboru tih intervala.
17: Skup

nema izolovanih tačaka.
Dokaz: Ako je

izolovana tačka skupa

, postoji

takvo da je
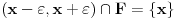
. Obzirom da je funkcija

lokalno polinomijalna na
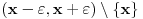
ona je prema 15 polinomijana na
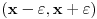
, što protivreči izboru tačke

.
18: Neka je

otvoren skup takav da je
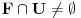
i neka je prirodan broj

. Postoji tačka
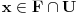
takva da je
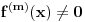
.
Dokaz: U skupu

možemo izabrati neki od intervala

na kome se
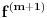
ne anulira. U suprotnom, pošto je na osnovu 3 skup
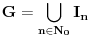
svuda gust, na osnovu neprekidnosti
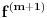
je
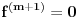
na celom skupu

, što je u suprotnosti sa
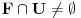
. Za tako izabrani

neka je

stepen polinoma kome je funkcija

jednaka na intervalu

. Obzirom da se
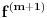
ne anulira na tom intervalu, važi

. Obzirom da je
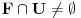
, interval

se ne svodi na

, pa mu barem jedan od krajeva pripada skupu

. Obeležimo ga sa

. Ukoliko je
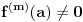
tvrđenje je dokazano (jer
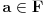
na osnovu 16). Pretpostavimo zato da je
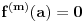
. Svakako je
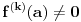
. Neka je

najmanji broj iz skupa
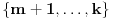
takav da je
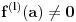
. Izaberimo okolinu
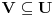
tačke

takvu da je
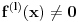
. To je moguće na osnovu 1. Obzirom da je za
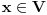
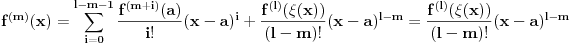
za neko
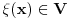
, važi
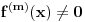
za sve
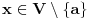
. Obzirom na 17 i
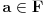
, tvrđenje sledi.
19:
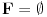
.
Dokaz: Pretpostavimo da je
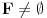
. Prema 18, obzirom da je
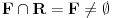
, možemo izabrati tačku
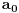
skupa
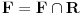
za koju je
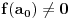
i na osnovu neprekidnosti

kompaktnu okolinu
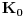
takvu da
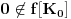
. Obzirom da je
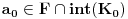
u okolini
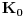
možemo izabrati unutrašnju tačku
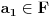
takvu da je
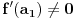
i na osnovu neprekidnosti
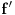
kompaktnu okolinu
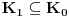
takvu da
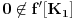
. Nastavljajući ovaj postupak, konstruišemo opadajući niz
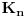
kompakata takav da
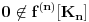
. Za
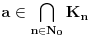
je
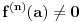
za sve
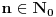
suprotno pretpostavci zadatka.
20.

je lokalno polinomijalna na

.
Dokaz: Na osnovu 19 je
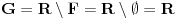
.
21.

je polinomijalna na

suprotno pretpostavci.
Dokaz: Na osnovu 11 i 20.
[Ovu poruku je menjao Nedeljko dana 09.06.2013. u 01:06 GMT+1]
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
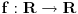 beskonacno diferencijabilna funkcija i neka za svako
beskonacno diferencijabilna funkcija i neka za svako 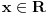 postoji
postoji 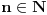 takvo da je
takvo da je 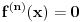 (
( -ti izvod funkcije). Pokazati da je tada
-ti izvod funkcije). Pokazati da je tada  polinom.
polinom.



 Pokazati da je f polinom
Pokazati da je f polinom