Citat:
number42:
cuj, hvala sto si izdvojio vreme da objasnis h-hipotezu, ali nisam skontao. verovatno mi fali znanja da bih to usvojio na taj nacin.
aj pokusaj da objasnis kao, ne znam, malom detetu ili nekoj babi s romanije
, sigurno cu razumeti.
Ajde da probam postupnije (kasnim nekoliko dana zato što sam bio u priličnoj gužvi, tek sad sam uspeo da odvojim malo vremena).
Neka je
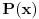
polinom s celobrojnim koeficijentima (to, pretpostavljam, znaš šta je); u celoj poruci govorimo isključivo o polinomima s celim koeficijentima.
E sad, nećemo posmatrati baš bilo kakav polinom, nego tražimo da taj polinom ispunjava određene uslove. Prvo, vodeći koeficijent treba da mu bude pozitivan (znači, polinom
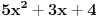
nam je OK, a polinom
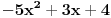
nije OK). Drugo, taj polinom treba da bude
nesvodljiv: to znači da se ne može napisati kao proizvod nekih polinoma manjeg stepena (znači, polinom
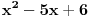
nije OK, jer ga možemo zapisati kao
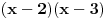
; s druge strane, polinom, primera radi,
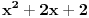
jeste OK, jer ga nikako ne možemo zapisati kao proizvod nekih polinoma manjeg stepena). Postoji i još jedan uslov, ali lakše mi je da njega uvedem malo kasnije. Onda H-hipoteza tvrdi da za beskonačno mnogo prirodnih brojeva
vrednost
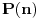
jeste prost broj. Recimo, jedan specijalan slučaj je tvrđenje da postoji beskonačno mnogo prostih brojeva
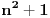
(ovo dobijamo kada za pominjani polinom uzmemo
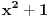
, što ispunjava sve tražene uslove).
Što se samih uslova tiče, oni su vrlo prirodni jer je jasno da bez njih ne možemo: primeti da, ako bismo dopustili i polinome s negativnim vodećim koeficijentimo (recimo, pomenuti
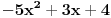
, tada će ovaj polinom za sve
od nekog momenta nadalje uzimati negativne vrednosti, pa je jasno da se tu nećemo previše 'leba najesti od prostih brojeva. Smisao drugog uslova takođe nije teško dokučiti: ako je, recimo,
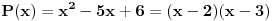
, tada koji god broj
ubacimo u ovaj polinom, dobićemo vrednost
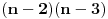
, a što već za
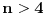
nikada nije prost prost broj jer je predstavljeno kao proizvod dva broja oba veća od
.
E sad, ako si ovo sve ukapirao, to nije kraj pošto smo sve ovo pričali preko samo jednog polinoma, ali H-hipoteza je formulisana i kada imamo koliko god polinoma, a ne samo jedan. Dakle, neka su
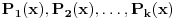
polinomi od kojih svaki ispunjava uslove koje smo nabrajali. Uz to, dodajmo i onaj treći uslov koji sam maločas pomenuo; citiraću ga najpre onako kako sam napisao i u prethodnoj poruci, a onda ćemo tumačiti šta to znači: „ni za jedan prost broj
nije ispunjeno da za svaki prirodan broj
broj
deli neku od vrednosti
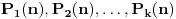
“. Hajde da se udubimo u ovo. Neka su dati polinomi
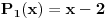
i
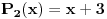
. Primetimo sada da, za ma koji prirodan broj
, jedna od vrednosti
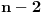
i
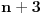
sigurno je parna, tj. deljiva sa
. Drugim rečima, za prost broj
ispunjeno je da, ma koji prirodan broj
da ubacimo u odabrane polinome, broj
deliće neku od vrednosti
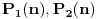
. Dakle, ovaj par polinoma nije u skladu s postavljenim uslovom (uslov kaže da ni za jedan prost broj
ne sme da se desi ono iz nastavka rečenice, a nama se to desilo za
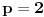
). Isto tako, ne sme se desiti da je uvek neki od brojeva
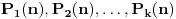
deljiv sa
(recimo, ako uzmemo tri polinoma:
,
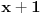
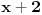
i
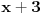
, oni krše postavljeni uslov), pa isto to za
, pa isto to za
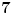
... E, konačno, H-hipoteza tvrdi da, kakvu god gomilu polinoma da imamo (ali da oni ispunjavaju zahteve koje smo naveli), onda postoji beskonačno mnogo prirodnih brojeva
za koje su brojevi
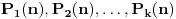
svi istovremeno prosti.
I sad ako uzmeš npr. polinome
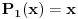
i
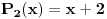
, tada se tvrdi da postoji beskonačno mnogo prirodnih brojeva
takvih da su i broj
i broj
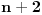
ujedno prosti, a ovo je upravo hipoteza o prostim blizancima.
Citat:
Nedeljko:
Bojane, da li ti primećuješ nerazumevanje materije od strane učesnika? Ako je odgovor pozitivan, pomozi im.
Evo, trudim se, nadam se da će sad biti uspešnije.
Citat:
number42:
a ovo bi moglo i da se uopsti, tako da bi izvedena hipoteza bila:
"izmedju bilo kog broja n i njegove dvostruke vrednosti 2n uvek je smesten barem jedan prost broj".
Ovo postoji i dokazano je. Potraži pod nazivom Bertranov postulat (negde se sreće i naziv Čebiševljeva teorema).
Ljubičice crvena, što si plava kô zelena trava.
Registrovani: 2 ( vjova, zeoN_Rider )
Re: da li postoji ova hipoteza?
evo naknadno sam video da je hipoteza koju sam dao u startu na pocetku- samo izvedena iz druge hipoteze kojoj tada nisam znao ime.
