Citat:
darkosos:
Rupa koja se popunjava parnim brojem (nastalim kao prost + 1), ne mora biti prava rupa, tj. da izmedju nema prostih brojeva, pa bih rekao da je Polinjakova hipoteza jaca od ove o kojoj se ovde prica... Dakle ako vazi Polinjakova, vazice i postavljena, ali ne i obrnuto.
Da, u pravu si. Polinjakova je jača već na osnovu toga što govori o rupama ma koje parne dužine (dok u našem slučaju pričamo samo o onim parnim brojevima koji su za

veći od prostog broja), no ovo što pominješ još je ozbiljnije pojačanje.
Citat:
number42:
znaci ovako: polinjakova hipoteza se moze preformulisati na sledeci nacin:
"za svaki prost broj (Pb1) postoji beskonacno mnogo nekih neparnih brojeva (2n+1) od kojih svaki pojedinacno kada se sabere sa Pb1 i brojem 1 daje neki prost broj (Pb2)".
Ne sasvim. Ovo što si ti napisao zapravo je očigledno tačno tvrđenje (fiksiraj broj Pb1, neka je Pb2 bilo koji prost broj veći od Pb1, i tada postoji neparan broj koji kad se sabere sa Pb1 i brojem 1 daje Pb2). Zapravo ono što ti zoveš Pb1 može biti bilo koji neparan broj, a ono gde ti pominješ proizvoljan neparan broj, e tu zapravo treba da stoji prost broj. Samo zameni ta dva pojma i dobićeš preformulaciju Polinjakove hipoteze kakvu si hteo, s tim što, kao što Darko reče, Polinjakova hipoteza još postavlja ograničenje da je Pb2
najmanji prost broj veći od Pbx.
Citat:
plague:
Edit: Nisam siguran da li je ovo potencijalni copyright problem, ako moderator smatra da jeste neka ukloni attachment.
Nažalost, ipak jeste. Ostaviću ga još neko vreme da skinu učesnici ove teme koji su zainteresovani, ali moraće da bude uklonjen posle toga.
Citat:
number42:
dok sam ovu prvu koliko toliko pohvatao, ovu drugu nisam skapirao, plus sto baca reference na jos neke druge stvari, tako da sam mislio ako imas vremena da ukratko objasnis ovu h-hipotezu, onako najprostije.
Dakle, posmatrajmo polinome
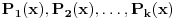
sa celobrojnim koeficijentima, s pozitivnim vodećim koeficijentom i nesvodljive nad prstenom celih brojeva. Neka su ovi polinomi takvi da ni za jedan prost broj

nije ispunjeno da za svaki prirodan broj

broj

deli neku od vrednosti
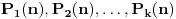
. Tada H-hipoteza tvrdi da postoji beskonačno mnogo prirodnih brojeva

takvih da su sve vrednosti
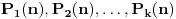
proste. Diksonova hipoteza je specijalan slučaj ove hipoteze, kada su svi posmatrani polinomi linearni.
To bi bilo vrlo ukratko, ali slobodno pitaj ako nešto iz ovog opisa treba bolje razjasniti, rado ću pomoći.
Ljubičice crvena, što si plava kô zelena trava.