Imamo zadatak ko neko treba da resi (na casu, takmicenju, ispitu, ...):
- Naci sve Goldbahove parove za brojeve od 41 do 49. Koliko ima takvih parova?
Kako ce to neko na najbolji nacin resiti ako na raspolaganju ima papir, olovku, hemijsku, dva lenjira i sestar (ono sto je inace dozvoljen pribor)?
Podrazumeva se da racunar nije dozvoljen (ali moze da ga napravi od raspolozivog materijala), ostala pomocna sredstva takodje (ako moze da ih napravi od raspolozivog materijala).
Ja sam izlozio moj pristup (koga nisam ja osmislio) kako bi mogli ovo da resimo (relativno jednostavno za nekih max 20 min)
- Erastotenovim sitom odredimo sve proste brojeve do 49 (mada realno moze i do 43 jer je 48=43+5 ali da ne bi gubili vreme oko razmatranja uzmemo veci broj odmah)
- geometrijskim izlozenim postupkom nadjemo resenja (da se ovo nacrta ne treba vise od 15-ak minuta).
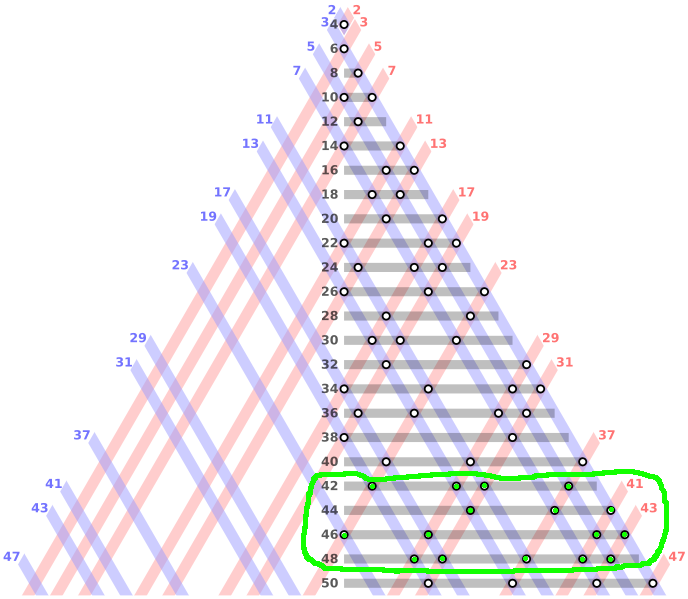
Postupak je univerzalan i za vece brojeve ali se potrebno vreme i prostor za crtanje geometrijski uvecavaju.
Ako moze siber da se nacrta i improvizuje za manje vreme onda ce to biti bolje resenje.
Pitanje je kako mozemo siber da nacrtamo (improvizujemo)?
Ja nisam uspeo da uocim princip (mada se detaljno nisam ni bavio time) ali nije uocljiv na prvi pogled kao ovo geometrijsko resenje.
Za neke inzenjerske potrebe siber ce biti upotrebljiv koliko i tablice, a racunar daleko delotvorniji.
A diskusija bi mogla da bude ipak malo konstruktivnija nego sto jeste.
Re: Goldbahovi parovi
Registrovani: 1 ( Fireborn )
