Postoji lema o zameni iz koje ovo sledi i to ne samo u konačnom slučaju.
Pretpostavimo da su sistemi oblika
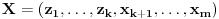
i
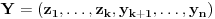
, pri čemu može biti i
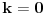
. Ako je
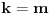
, onda tvrđenje neposredno sledi jer je
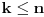
. Pretpostavimo zato da je
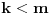
.
(1)
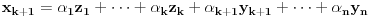
.
Obzirom da je sistem

linearno nezavisan, vektor
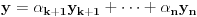
je različit od nule. Stoga postoji neko
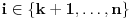
takvo da je
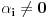
. Razmotrimo sistem
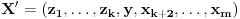
.
Na osnovu izbora vektora

svaki element sistema
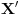
pripada linearnom omotaču sistema

.
Takođe, sistem
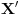
je linearno nezavisan. U protivnom važi
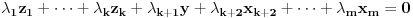
,
pri čemu bar jedan od skalara

nije nula. Zbog linearne nezavisnosti sistema

mora biti
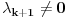
, pa je
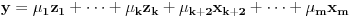
,
za neke skalare
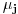
. Međutim, na osnovu (1) je
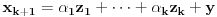
,
odnosno vektor
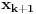
je linearna kombinacija preostalih vektora sistema

, što ej u suprotnosti sa njegovom linearnom nezavisnošću.
Neka je
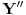
sistem koji se dobija od sistema

zamenom vektora na mestu

sa

. On ima isti lineani omotač kao

. Zaista, vektor

je linearna kombinacija vektora sistema

, a vektor
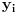
je linearna kombinacija vektora sistema
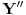
na osnovu izbora vektora

i
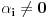
.
Neka je
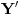
sistem koji se dobija zamenom vektora na mestima
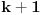
i

u sistemu
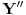
. On ima isti linearni omotač kao i sistem
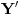
pa samim tim i

.
Međutim, sistemi
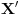
i
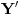
imaju prvih
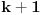
elemanata zajedničkih. Produžavajući ovaj postupak dolazimo do slučaja
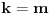
, koji je rešen.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.