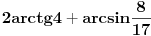Ako je
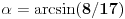
, koliko je
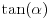
? Pa, prvo je
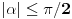
i
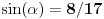
na osnovu definicije arkussinusa. No, onda možemo zaključiti da je
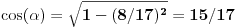
, pa je
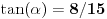
. Odatle i iz
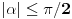
sledi da je
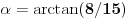
. Dakle, tebe zanima koliko je
.
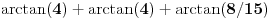
Neka je
.
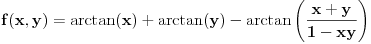
Obziom da je
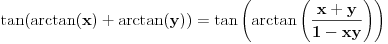
funkcija
sve tačke za koje je definisana slika u celobrojne umnoške broja
. No, domen joj se sastoji iz tri oblasti:
,
,
.
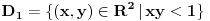
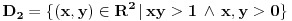
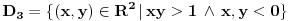
Obzirom da je funkcija
neprekidna, neprekidna slika povezanog skupa je povezan, a kodomen funkcije je potpuno nepovezan, ona je na svakoj od oblasti konstantna. Nije teško videti da se
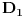
slika u nulu (jer se tačka
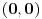
slika u nulu),
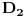
u
(npr. na osnovu limesa kada
), a
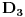
u
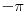
(na osnovu limesa kada
).
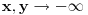
Stoga je
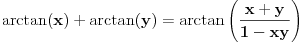
za
,
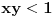
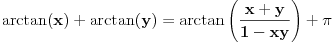
za
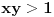
i
,
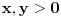
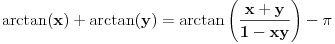
za
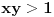
i
,
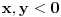
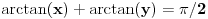
za
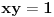
i
,
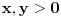
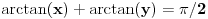
za
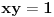
i
.
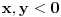
Poslednje dve relacije slede otuda što su tangensi oštrih uglova koji se dopunjuju do pravog recipročni i neparnosti tangensa.
Dakle,
,
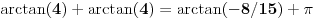
pa je ceo zbir jednak
.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Arkusi bez digitrona :)
Registrovani: 8 ( Blentostamin, _deran_, mjanjic, djoka_l, valjan, DUSKEZ, bachi, Turmen )
Re: Arkusi bez digitrona :)
Mada, nije mi baš jasan deo sa povezanim skupovima. Zaboravih da napomenem da se traži rešenje na nivou gradiva za srednju školu.
)
