• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 24.01.2002. Tri nova, nesto teža zadatka 13.04.2008. Ajmo kladionicari..... 05.05.2002. geometrija, 3 nova zadatka 01.06.2002. elegantno resenje ima li ga ? :) 13.01.2003. Nesto se zakomplikovalo 30.11.2003. Hitno trebam riješenje ovog zadatka 02.06.2004. Nuklearna fizika zadatak bitan 13.07.2004. Pomoć,ljudi! Trebam rješenje za 2 zadatka sa pr.. 01.10.2004. operacije sa skupovima Navigacija Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

zpezer Član broj: 36314 Poruke: 67 193.198.33.* +1 Profil matematika-postavka zanimljiva zadatka 06.10.2004. u 15:34 - pre 250 meseci Broj je sav od jedinica 111111111111 ....... ...... 11111111111 koliko ima jedinica ako je taj bro djeljiv sa 7, 11,13,............ svi prosti brojevi do 97 racunamo i 97 Odgovor na temu

gpreda Goran Predovic Kragujevac Član broj: 19087 Poruke: 74 195.252.81.* Sajt: alas.matf.bg.ac.yu/~mr990.. Profil Re: matematika-postavka zanimljiva zadatka 07.10.2004. u 13:36 - pre 250 meseci 19,709,529,840 Odgovor na temu

excrucio učenik, Slavonski Brod, Gimnazija Član broj: 176868 Poruke: 2 193.198.16.* +1 Profil Re: matematika-postavka zanimljiva zadatka 20.11.2012. u 09:18 - pre 151 meseci Kako dođe do toga??? Odgovor na temu

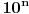
Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.3gnet.mts.telekom.rs. +2801 Profil Re: matematika-postavka zanimljiva zadatka 20.11.2012. u 12:38 - pre 151 meseci Broj koji se sastoji od jedinica iznosi . Obzirom da 9 nije deljivo ni sa jednim od navedenih prostih brojeva, da bi navedeni uslov bio zadovoljen, potrebno je i dovoljno da broj bude kongruentan jedinici po modulu svakog od tih prostih brojeva. 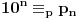Neka je za neki prost broj iz tog spiska za . 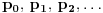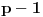Niz je periodičan sa periodom po maloj Fermaovoj teoremi. Međutim, to mu ne mora biti osnovni period. 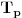Neka je osnovni period tog niza. Rešenje je svaki sadržalac broja . 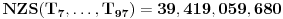[Ovu poruku je menjao Nedeljko dana 20.11.2012. u 23:35 GMT+1] Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

bigkandor Antispin Technologies Član broj: 300656 Poruke: 252 *.yourproxyhost.com. +228 Profil Re: matematika-postavka zanimljiva zadatka 20.11.2012. u 16:27 - pre 151 meseci Citat: Nedeljko: Broj koji je deljiv sa n jedinica iznosi Šta znači "Broj koji je deljiv sa n jedinica"? Da li to znači da je broj deljiv sa jednom jedinicom, deljiv sa drugom jedinicom, ..., deljiv sa n-tom jedinicom? Kolika je vrednost tih jedinica? Opet, ako je reč o brojevima iz skupa prirodnih brojeva onda je svaki broj deljiv sa koliko hoćeš jedinica i jedinica je u skupu prirodnih brojeva jedinstvena (bar je bila). Odgovor na temu

excrucio učenik, Slavonski Brod, Gimnazija Član broj: 176868 Poruke: 2 193.198.16.* +1 Profil Re: matematika-postavka zanimljiva zadatka 20.11.2012. u 16:45 - pre 151 meseci Citat: Nedeljko: Niz je periodičan sa periodom po maloj Fermaovoj teoremi. Međutim, to mu ne mora biti osnovni period. Neka je osnovni period tog niza. nisam siguran da sam shvatio što ti je točno niz... Citat: Rešenje je svaki sadržalac broja . ne razumijem što misliš reći Odgovor na temu

darkosos Darko Šoš Beograd Član broj: 5053 Poruke: 1131 95.180.55.* +64 Profil Re: matematika-postavka zanimljiva zadatka 20.11.2012. u 17:34 - pre 151 meseci Evo nekih primera: npr. koliki treba da bude broj oblika 111...1 (n jedinica) da bi bio deljiv sa na primer 7? Posto je zakljucujemo da treba da da ostatak 1 posle deljenja sa p. Prema navedenoj teoremi je pa znaci da je . Da proverimo, trebalo bi da je 111111 (6 jedinica) deljivo sa 7: i zaista, . Ono sto malo komplikuje pricu jeste da to ne mora biti najmanji takav broj. Evo na primer za 13: 111111111111 (12 jedinica) jeste deljivo sa 13, ali to vazi i za 111111 (6 jedinica). Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.3gnet.mts.telekom.rs. +2801 Profil Re: matematika-postavka zanimljiva zadatka 20.11.2012. u 22:40 - pre 151 meseci Citat: bigkandor: Šta znači "Broj koji je deljiv sa n jedinica"? Lapsus. Ispravljeno je. Citat: excrucio: ne razumijem što misliš reći Pa je ostatak pri delenju broja sa . Na primer, , , , , , , , , , , , , ... Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu