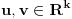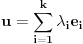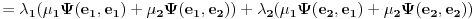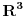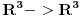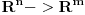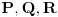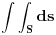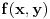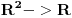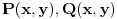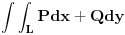[es] - Površinski integrali II vrste

Sonec

Član broj: 284879
Poruke: 892

+332 Profil

Površinski integrali II vrste - teorija

^{21.06.2012. u 23:30 - pre 156 meseci}

Prikacio sam uz poruku pitanje.

EDIT: Cekaj! Izgleda da sam shvatio! Ono je dokaz da oni funkcionali cine jednu bazu vektorskog prostora svih bilinearnih antisimetricnih funkcionala. Neka mi neko potvrdi/demantuje ovo.

_{[Ovu poruku je menjao Sonec dana 22.06.2012. u 00:59 GMT+1]}

Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.

Prikačeni fajlovi

Povrsinski_integrali_druge_vrste.pdf - 116.13k

Odgovor na temu

Nepoznat covek
Student

Član broj: 296039
Poruke: 74
*.dynamic.isp.telekom.rs.

+4 Profil

Re: Površinski integrali II vrste - teorija

^{21.06.2012. u 23:57 - pre 156 meseci}

Jao, kako ovo prevazilazi sve što ja znam puta beskonačno

Nego, šta si ti upisao, pa radiš ovakve stvari. Izvinjavam se ako spamujem.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Površinski integrali II vrste - teorija

^{21.06.2012. u 23:57 - pre 156 meseci}

Nemam sada vremena da odgovaram u celini, ali površ ima najviše dve klase ekvivalencije parametrizacija, a najmanje jednu. Mebijusova traka nema dve i onda se kaže da ona nije orjentabilna.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892

+332 Profil

Re: Površinski integrali II vrste - teorija

^{22.06.2012. u 00:32 - pre 156 meseci}

Dobro Nedeljko, kad budes imao vremena ti odgovori.

Citat:

Nedeljko: površ ima najviše dve klase ekvivalencije parametrizacija, a najmanje jednu.

Jesi ovde mislio na klase ekvivalencije orijentacije ili bas parametrizacije? Ako parametrizacije, onda mi to nije bas najjasnije.

Znam, primer Mebijusove trake je dosta poznat. I editovao sam poruku (ne pdf), pogledaj to da li ima smisla ako mozes.

Citat:

Nepoznat covek:Nego, šta si ti upisao, pa radiš ovakve stvari.

Matematicki fakultet u Beogradu.

Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.static.isp.telekom.rs.

+64 Profil

Re: Površinski integrali II vrste - teorija

^{22.06.2012. u 08:20 - pre 156 meseci}

Taj prvi deo mislim da se dobija kada se zameni da su argumenti operatora zapravo vekrtori koji se mogu izraziti preko standardne baze

(to si oni e vektori koje si pomenuo).

Dakle nesto ovako, ako

, onda se oni mogu napisati kao

pa se na njih primeni bilinearnost funkcionala

. Kad se to raspise, trebalo bi da se dobije ta prva jednakost. Evo recimo za k=2:

Itd... kad se ovo jos malo izmnozi, dobijas tu formu koja se trazi, dakle ostaju neki koeficijenti koji mnoze

. Moze ovo verovato da se napise i "tehnickije" u opstem slucaju (dakle bez raspisivanje) ali mislim da je dobro da se zna sta se desava pod haubom :) I podrzavam tvoj napor da razumes materiju na prirodan nacin...

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Površinski integrali II vrste - teorija

^{22.06.2012. u 09:48 - pre 156 meseci}

Kako je kad odgovaram u sitne sate...

Neorjentabilne površi kao Mebijusova traka nemaju atlas, a stavo tačno dve orjentacije atlasa (ako uopšte postoje atlasi) je OK.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892

+332 Profil

Re: Površinski integrali II vrste - teorija

^{22.06.2012. u 14:38 - pre 156 meseci}

Citat:

Nedeljko: a stavo tačno dve orjentacije atlasa (ako uopšte postoje atlasi) je OK.

Ne razumem sta si rekao.

I jos jednom, jel mi dobro ono sto sam spomunuo u EDIT-u?

Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.54.*

+64 Profil

Re: Površinski integrali II vrste - teorija

^{22.06.2012. u 20:32 - pre 156 meseci}

Mislim da siu pravu, sto se tice edit-a, da se zapravo pokazuje ta prva recenica posle nabrajanja osobina funkcionala.

Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892

+332 Profil

Re: Površinski integrali II vrste - teorija

^{22.06.2012. u 21:00 - pre 156 meseci}

Ma jesam. To je to.

Al stvarno, jel ima neka pricica sta nam predstavlja orijentacija neke povrsi? (znam za ono sto sam napisao, al hteo bih obicnim recima da se kaze)

Kakva su tumacenja orijentacije, pretpostavljam da fizicari imaju neku svoju interpretaciju.

Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.

Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892

+332 Profil

Re: Površinski integrali II vrste - teorija

^{22.06.2012. u 21:14 - pre 156 meseci}

Hocu ovo da pitam. Koja je razlika sustinska izmedju povrsinskog integrala I i II vrste. Mi u oba slucaja racunamo povrsinu (zar ne ?). Da li je to "samo" u nacinu na koji to radimo, pa u zavisnosti od nacina, razvijamo posebno jednu i drugu teoriju?

I mislim da sam shvatio orijentaciju. Dakle, kada radimo recimo zadatak i odredimo jednacinu normale na povrs mi nismo odredili jedinstveno tu normalu, jer smo samo nasli pravac, ali ne i smer te normale. I tu onda upada u pricu orijentacija (jer svaka povrs ima jedinstvenu orijentaciju u

(recimo da radimo tu)) i u zavisnosti od orijentacije (kako nam je zadano da je orijentisana povrs) mi gledamo da li nam se poklapa smer normale sa tom orijentacijom, i tu uskace plus ili minus, u zavisnosti da li treba da obrnemo smer ili ne.

Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.

Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892

+332 Profil

Re: Površinski integrali II vrste - teorija

^{22.06.2012. u 22:50 - pre 156 meseci}

U stvari nije ni vazno. Bas sam glup. Treba da se ponasam kao i svi ostali (velika velicina), bitno je da u datom trenutku prevarimo profesora, a i sebe, a sad, sto ne znamo zasto je to tako, jaka stvar. Bitno je poloziti ispit i dobiti diplomu, a znanje je ipak na drugom (mozda i na nekom nizem) mestu. Razocaran sam.

Ne mogu vise da ucestvujem na ovom forumu. Osecam se bedno i ponizeno. Dovidjenja.

Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.54.*

+64 Profil

Re: Površinski integrali II vrste - teorija

^{23.06.2012. u 07:09 - pre 156 meseci}

Kakve su to malodusnosti? Ne razumem zasto se tako osecas? Zbog studenata koji prolaze a ne zanima ih nista osim da poloze i idu dalje?

Svakako postoje dve vrste ljudi, sto se ovoga tice: oni koji studije vide samo kao sredstvo da dodju do cilja i oni koji zele da znaju (neki od ovih prvih postaju i asistenti). Ali to je tako, bilo je i bice tako... Dakle svet funkcionise tako kako funkcionise hteli mi to ili ne, tj. bez obzira na nase licne moralne norme. Mudrost je onda naci svoje mesto u svemu tome...

Rekao sam ti vec ranije, mislim da je super sto zelis da razjasnis materiju i da ti to bude jasno na neki prirodan nacin, dakle ispricano nekim jednostavnim jezikom. I ja isto imam tu potrebu da stvar svedem na nesto prosto, iako mozda celina ume da bude slozena. Ali rekao bih da mozak izvrsava i veoma komplikovane operacije a da toga nismo ni svesni - evo i sad se cudim kako deca (tj. svi mi) propricaju a da to ne uce na klasican nacin i da prakticno nemaju pojma ni gde su ni sta su, pa ni sta je jezik :)

Sta hocu da kazem? Pa postoje mnoge stvari koje su nam "prirodne" jer su nastale na osnovu iskustva, ili su ugradjene u DNK, mozda ne moramo logicki ni da ih ispitamo, a koje se mogu zato iskoristiti, koristeci analogiju, da oni delovi nauke koji izgledaju prekomplikovano postanu jasni. To je ono sto si ti nazvao "pricica". E pa eto, to moze da bude tvoj cilj: da potrebom koju imas, dodjes do jednostavnih pristupa. Naravno, najbolje ces to iskoristiti kao asistent ili profesor - to je dug put, jasno. Meni je npr. dovoljno da na ovom forumu pomognem nekom svojim pristupom, jer se ne bavim naukom.

A ti si pokazao da mozes, a pre svega hoces, i zaista ne vidim zasto bi sada odustajao?

Odgovor na temu

markob15
Marko Berar
Beograd

Član broj: 156982
Poruke: 79
*.adsl.eunet.rs.

+11 Profil

Re: Površinski integrali II vrste - teorija

^{24.06.2012. u 02:49 - pre 156 meseci}

Citat:

Hocu ovo da pitam. Koja je razlika sustinska izmedju povrsinskog integrala I i II vrste

Pa laički rečeno, površinski integral I vrste tiče se skalarnih funkcija (polja), odnosno funkcija oblika

ili bolje receno

(kao što je npr. f-ja temperature, koja svakoj t-ki prostora dodeljuje konkretan br - temperaturu u toj t-ki.. )

Dok se površinski integral II vrste bavi vektorskim funkcijama (poljima) t.j. funkcijama oblika

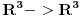
odnosno

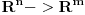
(kao sto je npr. funkcija gravitacije koja svakoj tacki prostora, dodeljuje vektor gravitacione sile koja deluje na tu tacku)

U slucaju povrsinskog integrala II vrste najcesce zapisanog u obliku:

upravo su

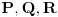
komponente vektorske funkcije (polja)

Kao što rekoh laičiki rečeno, mislim da je to suštinska razlika između integrala I i II vrste, kako površinskog tako i krvolinijskog.
Dakle I vrsta se bavi skalarnim a II vrsta vektorskim funkcijama.

Citat:

Mi u oba slucaja racunamo povrsinu (zar ne ?)

pa i ne baš, stvar je bliža zapremini nego površini (buduci da se povrsinski integ. svodi na visestruki) ali ne verujem da je baš ispravno govoriti na takav način, budući da se sve dešava u višim dimenzijama.
Pride ako te ime buni, krivolinijski odnosno povrsinski integrali dobili su ime po onome NAD cim se vrsi integracija a ne STA izracunava. (krivolinijski nad krivom, povrsinski nad povrsi)
(Moguce je pak, izracunati povrsinu povrsi

u slucaju:

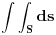
, dakle kada "nema" funkcije koja se "integrali".)

Primera radi, krivolinijski integral I vrste funkcije

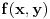
, dakle oblika

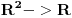
nad krivom

u Oxy ravni,

prakticno bi mogao da se shvati kao povrsina (zavesa) odredjena sa jedne strane krivom a sa druge tom funkcijom(koja ce biti neka povrs).

http://www.youtube.com/watch?v=_60sKaoRmhU

Ovo je vrlo teorijski neutemeljeno, samo koristim kao primer vizuelizacije. Stvar je u tome sto se u visim dimenzijama ne moze praviti ovakva vizualizacija pa samim tim pojmovi povrsina/zapremina gube na smislu.

Dok bi, recimo krivolinijski integral II vrste vektorske funkcije

dakle oblika

(gde su P, Q funkcije po x, y t.j.

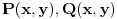
) po krivoj

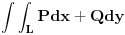
predstavljao rad sile

koja deluje na materijalnu tacku u prostoru indukujuci njeno pomeranje duz pravca

.

http://www.youtube.com/watch?v=t3cJYNdQLYg&feature=relmfu

evo malo i primera primene povrsinskih integrala:
http://www.math24.net/physical...ions-of-surface-integrals.html

Nadam se da sam doprineo :)

_{[Ovu poruku je menjao markob15 dana 24.06.2012. u 04:17 GMT+1]}

Odgovor na temu