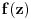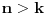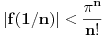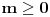Srodne teme

03.10.2003. Prilagodjavanje rezolucije
06.03.2013. zadaci za takmicenja
06.09.2004. Pitanje iz mat. za 5. r.OŠ HITNO
01.03.2005. Pravilnik takmicenja iz matematike
08.04.2005. metodika nastave matematike
27.04.2005. Zadaci sa reg. takmičenja iz matematike
26.06.2008. zadatci iz matematike
05.02.2017. Problemi u nastavi matematike
15.07.2006. casovi iz diskretne matematike i linearne algebre
29.10.2006. Potrebna zbirka zadataka iz matematike.

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Pitanje o unapređenju nastave matematike

[es] :: Matematika :: Pitanje o unapređenju nastave matematike

Strane: 1 2 3

[ Pregleda: 7755 | Odgovora: 50 ] > FB > Twit

Autor

igorpet

Član broj: 18898
Poruke: 553
*.dynamic.isp.telekom.rs.

+46 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 10:36 - pre 156 meseci}

Citat:

Nedeljko: igorpet

Što se tiče zadatka koji su jako slični zadatku koji je rađen na vežbama, na taj način se na ispitu proverava (skoro) neupotrebljivo znanje, osim ako je taj zadatak nešto što će se posle studija tipičo pojavljivati. Dakle, Bojan i ja zastupamo stav o prenošenju i traženju upotrebljivog znanja.
...

Da li to znaci da se na vezbama uglavnom rade zadaci koji daju neupotrebljivo znanje? Ako je tako onda si u pravu.
Ali moje pitanje je onda zasto je to tako, zasto se na vezbama ne rade kvalitetniji zadaci.

Ako mislis da je bespredmetno davati na ispit nesto sto je vec radjeno i obradjeno onda mislim da nisi u pravu jer ako se na vezbama i predavanjima osim elementarnih i uvodnih rade i kvalitetniji primeri zadataka zasto bi onda bilo lose davati takve ili slicne zadatke.
Ako je cilj predmeta ili materije sticanje upotrebljivog znanja onda neka sve bude u tom pravcu pa i ispitni zadaci, ako je vec takav koncept.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 11:00 - pre 156 meseci}

Citat:

igorpet: Da li to znaci da se na vezbama uglavnom rade zadaci koji daju neupotrebljivo znanje? Ako je tako onda si u pravu.
Ali moje pitanje je onda zasto je to tako, zasto se na vezbama ne rade kvalitetniji zadaci.

Kakve su vežbe, to zavisi od toga ko ih drži i kome. Može na vežbama da se uradi hiljadu najkvalitetnijih zadataka, ali malo je verovatno da će se u praksi tipično sretati zadaci koji su vrlo slični nekom od tih hiljadu zadataka. Na vežbama student treba da se osposobi za rešavanje što više problema, a ne za rešavanje tih hiljadu koji su rađeni na vežbama. Dakle, to je ona priča o profesoru Caji sa ETF-a. On je naučio studente da reše sto zadataka, ali ih nije naučio elektroniku, dok ona američka knjiga uči čitaoca elektronici, a ne rešavanju zadataka iz knjige. Znači, daje u ruke alat za rešavanje široke klase zadataka. Naravno, visokoobrazovan čovek ne treba da zna da rešava samo potpuno šablonske zadatke, već i da razmišlja, koliko-toliko. Ne mislim da zadaci treba da budu za olimpijadu, ali da proveravaju upotrebljivo znanje.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

igorpet

Član broj: 18898
Poruke: 553
*.dynamic.isp.telekom.rs.

+46 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 11:30 - pre 156 meseci}

Citat:

Nedeljko: Kakve su vežbe, to zavisi od toga ko ih drži i kome. Može na vežbama da se uradi hiljadu najkvalitetnijih zadataka, ali malo je verovatno da će se u praksi tipično sretati zadaci koji su vrlo slični nekom od tih hiljadu zadataka. Na vežbama student treba da se osposobi za rešavanje što više problema, a ne za rešavanje tih hiljadu koji su rađeni na vežbama. Dakle, to je ona priča o profesoru Caji sa ETF-a. On je naučio studente da reše sto zadataka, ali ih nije naučio elektroniku, dok ona američka knjiga uči čitaoca elektronici, a ne rešavanju zadataka iz knjige. Znači, daje u ruke alat za rešavanje široke klase zadataka. Naravno, visokoobrazovan čovek ne treba da zna da rešava samo potpuno šablonske zadatke, već i da razmišlja, koliko-toliko. Ne mislim da zadaci treba da budu za olimpijadu, ali da proveravaju upotrebljivo znanje.

Pa upravo iz tih razloga imamo lose, dobre i odlicne porfesore. Zadaci trebaju da demonstriraju upotrebljivost predmeta, bilo da su zadaci sa ispita bilo da su zadaci sa vezbi. Deluje mi da ti razdvajas zadatke na ispitne i one koji se rade na vezbama. Po meni i ispitni zadaci bi trebali biti koncepcijski i tezinski u skladu sa zadacima na vezbama, osim za visoke ocene gde se malo "dublje" proverava poznavanje materije.

Kazes da ispitni zadaci mozda ne bi trebalo da budu bas olimpijski ali da proveravaju znanje. Ja mislim da bas svi zadaci proveravaju znanje samo sto neki elementarni proveravaju elementarno a takmicarski vrlo visoko znanje. A ocena treba da bude neko objektivno merilo stecenog znanja, 6-ica otprilike znaci elementarno i deo srednjeg znanja a u nekoj gradaciji 10-ka bi trebala da znaci jako visoko znanje, ali to oko 10-ke mi nije bilo nikad bas najjasnije, imao sam ih imao nekoliko, jer licno nisam smatrao da bas briljiram tom materijom iako sam dobro pripremljen izasao na ispit ali u okviru potpuno standardne literature, deluje mi da za 10 treba otici malo dalje sa literaturom i znanjima, ali to je ta sarolikost u kriterijumima.

I ja sam zavrsio ETF, nisam imao cast da licno upoznam Caju jer nisam studirao na Beogradskom univerzitetu, ali bilo je i kod mene par profesora koji su imali da kazemo malo cudne kriterijume, po mom skromnom misljenju, mada licno nikad nisam imao problema sa ispitima i profesorima i ni jedan ispit nisam polagao vise od 3 puta. Ali licni utisci studenata o profesorima nisu uvek bas najmerodavniji, a narocito dok ne poloze taj ispit. Sa neke distance, posle zavrsetka fakulteta, moze da se napravi mnogo bolja i kvalitetnija komparacija predavaca.

U nekom pedagoskom smislu, kad sa ove 12-togodisnje distance pogledam, profesori koji su imali visoko apsolutno znanje i bili "duboko" u materiji su cesce (mada ne i obavezno) losije stojali sa pristupom u objasnjavanju materije a narocito zadataka jer su uvek nesto podrazumevali, isli nekim precicama i bilo je tesko ispratiti ih na casovima. Valjda kad znas mnogo oni elementarni zadaci ti deluju potpuno smesno, oni iz srednje kategorije nedovoljno ozbiljno pa su uvek, cini mi se, imali problem da pogode tezinu ispitnih zadataka, na "stetu" studenata. A studenti ko studenti ... kako god bilo, losim studentima je uvek kriv predavac, oni bolji i odlicni mogu nesto bolje da oforme kriterijum ali uvek je bilo: pa kako mi nije dao 10 a sve sam znao ...

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 12:08 - pre 156 meseci}

Citat:

igorpet: U nekom pedagoskom smislu, kad sa ove 12-togodisnje distance pogledam, profesori koji su imali visoko apsolutno znanje i bili "duboko" u materiji su cesce (mada ne i obavezno) losije stojali sa pristupom u objasnjavanju materije a narocito zadataka jer su uvek nesto podrazumevali, isli nekim precicama i bilo je tesko ispratiti ih na casovima. Valjda kad znas mnogo oni elementarni zadaci ti deluju potpuno smesno, oni iz srednje kategorije nedovoljno ozbiljno pa su uvek, cini mi se, imali problem da pogode tezinu ispitnih zadataka, na "stetu" studenata. A studenti ko studenti ... kako god bilo, losim studentima je uvek kriv predavac, oni bolji i odlicni mogu nesto bolje da oforme kriterijum ali uvek je bilo: pa kako mi nije dao 10 a sve sam znao ...

Ja mislim da ti profesori za koje smatraš da su imali "duboko znanje" zapravo nisu imali pojma. To je na primer Caja. On je bio klikeraš da reši razne slučajeve nekim svojim dosetkama, ali nije imao znanje o opšttem u elektronici, pa stoga nije mogao ni da ga prenese. E, onda kada studenti vide kako je on rešio sto zadataka dosetkama, pomisle "ala je ovaj pametan. Kakav genije", a u stvari je suština u tome da on nije imao opšte znanje elektronike, pa je knjiga ispala takva. Caja bi sa tim svojim dosetkama bio verovatno odličan inženjer, ali za profesora treba mnogo više od toga.

Takođe, pravi genijalci ne vide nikakav izazov u rešavanju ispitnih zadataka, niti osećaju potrebu da se prave pametni pred studentima. Takav kompleks obično imaju oni koji su tanki sa znanjem, a ispasti pametan pred studentima je najmanji problem.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

igorpet

Član broj: 18898
Poruke: 553
*.dynamic.isp.telekom.rs.

+46 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 12:36 - pre 156 meseci}

Citat:

Nedeljko: Ja mislim da ti profesori za koje smatraš da su imali "duboko znanje" zapravo nisu imali pojma...

Pa bilo je onih koji su imali i realno znanje, za konkretnog profesora koga pominjes ne znam tacno pa ne mogu nista ni da kazem.
Ali hteo sam da kazem da neko ko mnogo zna ne oseca potrebu da se bavi nekim osnovnim stvarima u zadacima ili to jednostavno preskace jer je po njemu to potpuno ocigledno. Nesto sto je za njega ocigledno za vecinu studenata nije i kad ti neko uradi zadatak u 10 redova jer podrazumeva ostalih 50 onda se nadjes u problemu. Ne pricam samo o ispitnim zadacima nego i o onim sa predavanja, vezbi i slicno.
I ne govorim o nekim "demonstracijama znanja" predavaca nego o obicnim predavanjima i izlaganjima.

Ja razumem da on nema motiv da se bavi tim, za njega sitnim i potpuno ociglednim stavarima, ali izmedju motiva i obaveze ja bih ipak bio za to da je predavac tu zbog studenta i da njega nesto nauci. Ko sto kaze ona narodna: Nije znanje znati vec je znanje znanje drugom dati. I uvek je teze drugog nesto nauciti nego sam shvatiti, ako je taj drugi po znanju dosta "ispod" tebe. I profesorski zanat obicno ne podrazumeva samo znanje vec i dosta vise od toga, da uspes da postepeno i jasno uvodis nekog u materiju, da ides od ociglednog ka manje ociglednim, da izbor zadataka bude takav da se postepeno i sistematski ulazi u problematiku, da "se spustis" na nivo studenta i shvatis sta to njemu nije jasno i da to objasnis i kad te niko nista ne pita, da na osnovu iskustva i gresaka studenata sistematizujes neku oblast sa akcentima na tim "problemima- cakama" i jos mnogo toga. Npr. to sto studenti zovu "caka" obicno je samo manje ocigledna i potpuno normalna stvar za predavaca u zadatku ili nekog ko ima iskustva sa tim.

To je skoro uvek mnogo napornije i teze nego jednostavno resiti neki konkretan problem-zadatak. Retki su oni koji sve to mogu bez nekog velikog talenta i sklonosti ka tome. Ostali moraju imati dosta volje i voleti svoj poziv da bi stigli do tog nivoa.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 13:16 - pre 156 meseci}

Težište rasprave je skrenulo na unapređenje ispitnih metoda.
Treba dozvoliti korištenje literature.U moje vrijeme to je rađeno prešutno.Svi smo pravili sitno ispisane puškice, šalabahtere ,harmonike...
Tu bi zapisali neke osnovne formule,rutine i sl.Redovno su profesori i asistenti na to gledalo kroz prste,sem rijetkih policijski orjentiranih.
Dakle umjesto puškica studenti bi mogli napraviti solidnu podlogu,ekstrakt iz predavanja,umjesto da to nauče napamet.Individualno pravljenje ovih papira je od velike koristi za savlađivanje gradiva.Naravno da će biti lijenština koji će koristiti tuđe podloge,uglavnom bezuspješno.
Računari na ispitu - NE!Kao ni šestar-lenjir-trokut,ni log.tablice,ni log.računaljka-šiber,ni kalkulator ili neki drugi alati. Ali treba obavezno uvesti kolokvijum rješavanja zadataka na računarima sa bar jednim mat.programom.I to kao uslov izlaska na ispit.
Ne treba škrtariti sa najvećom ocjenom (10).Slučajni lapsus,greška zbog vremenske stiske i sl treba tolerisati.Ali za 6 treba pažljivo odvagati.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 17:42 - pre 156 meseci}

igorpet

Najbolji su oni univerziteti na kojima se stekne najveće znanje, pa ti vidi ko predaje na vrhunskim univerzitetima. Sve sam naučni krem iz svojih oblasti. Po tvojoj teoriji bi ti univerziteti bili najgori.

zzzz

Ne radi se samo o ispitnim metodama, već i o ciljevima nastave. Dakle, o tome kakvo znanje treba prenositi i šta je to upotrebljivo znanje. Kalkulator će mi reći da je ln(2)=0.693... Do tog sam rezultata mogao doći i razvojem logaritma u Tejlorov razvoj u okolini tačke 1, pa računanjem logaritma u tački 1/2 i na kraju promenom znaka. Ali, čemu sve to? Naravno da treba znati koristiti Tejlorov razvoj, ali onda neka zadatak bude odgovarajući. Čemu će na kraju meni služiti moje znanje računanja logaritma na ruke? Ako znam da koristim Tejlorov razvoj, ja ću to svakako znati. No, ima i drugih načina da se proveri sposobnost upotrebe Tejlorovog razvoja. Ako profesor ne zna da smisli takve zadatke, onda on ne zna čemu služi Tejlorov razvoj.

Evo, recimo, svojevremeno sam na ispitu iz kompleksne analize imao zadatak da odredim sve kompleksne diferencijabilne funkcije

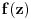
na otvorenom jediničnom disku za koje postoji prirodan broj

takav da za svako

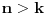
važi

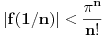
. Lepo se zna da su sve diferencijabilne kompleksne funkcije kompleksne promenljive sa otvorenim domenom analitičke, tj. da su beskonačno diferencijabilne i da njihov Tejlorov razvoj u okolini bilo koje tačke konvergira u nekoj okolini te tačke baš toj funkciji, napiše se funkcija u obliku stepenog reda koji je konvergentan ka njoj u nekoj okolini nule, ako funkcija nije nula, postoji prvi koeficijent Maklorenovog razvoja koji nije nula, pa postoje ceo broj

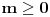
i neprekidna funkcija

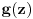
takve da je

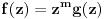
i

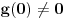
, ali onda nejednakost iz zadatka ne može da važi za beskonačno mnogo prirodnih brojeva

i gotovo - jedina funkcija koja ispunjava uslove zadatka je nula funkcija. Mala varijacija ideje dokaza teoreme jedinosti. To je primer ne preteškog zadatka zadatak koji provereva sposobnost primene Tejlorove teoreme iz kompleksne analize.

U takvom zadatku ti nikakav kompjuter ne bi pomogao. No, mogući su i zadaci u kojima bi ti kompjuter pomogao ako znaš ono što zadatak proverava.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

igorpet

Član broj: 18898
Poruke: 553
*.dynamic.isp.telekom.rs.

+46 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 18:13 - pre 156 meseci}

Citat:

Nedeljko: igorpet
Najbolji su oni univerziteti na kojima se stekne najveće znanje, pa ti vidi ko predaje na vrhunskim univerzitetima. Sve sam naučni krem iz svojih oblasti. Po tvojoj teoriji bi ti univerziteti bili najgori.

Vrhunske svetske univerzitete pohadjaju obicno studenti koji imaju odlicna predznanja, tamo prosecni i ispodprosecni djaci ne mogu da stignu, sto zbog materijalnih a sto zbog intelektualnih mogucnosti.
Takvi studenti obicno imaju znanja na samom startu mnogo vise od prosecnih koji dodju do sredine studija.
Studenti koji upisuju te fakultete su sposobni da prate predavanja tih profesora jer imaju jako predznanje steceno na raznim pripremam, takmicenjima i sl.

Npr. mislis li da ce Teodor fon Burg imati problema da proprati bilo koje predavanje vezano za matematiku na bilo kom fakultetu?
Taj i slican nivo znanja upisuje te univerzitete koje spominjes i daleko je to od nekog proseka pa i nije bas za poredjenje.
A mozda i ti profesori shvataju svoju ulogu pa se malo vise potrude i kad im nije do toga, a na kraju krajeva motivisanu su prilicno jer njihovi godisnji prihodi se mere stotinama hiljada dolara za tu ulogu koju imaju u obrazovanju.
A eto npr. Bojan ti moze reci koliko je on "motivisan" od strane drzave ili univerziteta za ono sto radi. Kod nas je uglavnom sve prepusteno licnom entuzijajzmu, sposobnostima i mozda zeljama gde se licni interes stavlja u drugom planu. Ali zato nemamo puno kadrova koji su spremni za sve to.

Po mojoj teoriji kad bi vrhunski univerziteti placali svoje profesore koliko i nasa drzava, kad bi radili u slicnim uslovima i kad bi politika i nacin upisa bila slicna nasem mislim da bi bili duplo gori po rezultatima od nasih univerziteta.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 18:23 - pre 156 meseci}

A ja imam drugare koji nisu Teodori fon Burgovi, a doktorirali su na mnooogo boljim mestima od bilo kog srpskog.

Najveći problem je kad nemaš šta da preneseš.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

igorpet

Član broj: 18898
Poruke: 553
*.dynamic.isp.telekom.rs.

+46 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 18:42 - pre 156 meseci}

Citat:

Nedeljko: A ja imam drugare koji nisu Teodori fon Burgovi, a doktorirali su na mnooogo boljim mestima od bilo kog srpskog.
Najveći problem je kad nemaš šta da preneseš.

Mi imamo odlicne pojedince, sposobne, radne, sa visokim intelektom i oni bi mogli podici kvalitet brzinom svetlosti ali sta nemamo ... nemamo sistem koji ce stati iza njih, nemamo ekonomiju koja bi ih podrzala i privredu i institute koji bi ih uposlilili i iskoristili u intelektualnom smislu.
O motivima studenata za studiranjem i profesora za predavanjem i sta ciniti posle sudija pricali smo jednom u nekim diskusijama, mislim da se nista nije promenilo niti ce skorije.

Ali sve ovo nije razlog da se pojedinci ne trude da rade najbolje sto mogu i kako mogu, i da ne unapredjuju nastavu, ali valjda je potpuno jasno zasto su oni u velikoj manjini.

Odgovor na temu

berazorica

Član broj: 246954
Poruke: 165
*.mynsn.net.

+127 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 19:52 - pre 156 meseci}

Citat:

Bojan ti moze reci koliko je on "motivisan" od strane drzave ili univerziteta za ono sto radi. Kod nas je uglavnom sve prepusteno licnom entuzijajzmu, sposobnostima i mozda zeljama gde se licni interes stavlja u drugom planu. Ali zato nemamo puno kadrova koji su spremni za sve to.

Ne. Pre bih rekla da ti on i njegove kolege mogu reći sa koliko entuzijazma se može raditi sa studentima kakvi se ovih godina upisuju na fakultet. Doduše, i to je sistemska greška - fakulteti su plaćeni po broju studenata, pa onda traže način da ih privuku i zadrže i naprave kakvu-takvu normalnu prolaznost... ali sve to prežvakano je na temi "Kuda ide današnje obrazovanje?"

"We are mathematicians, we are happy when we have a problem!"

Odgovor na temu

zivanicd
Dejan Zivanic
KLADOVONET ISP
Kladovo

Član broj: 137218
Poruke: 1129
*.zivanic.com.

Sajt: www.kladovo.net

+139 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 19:56 - pre 156 meseci}

Postovani profesori.

Iz mog iskustva kazem da ostavite studente da sve rade rucno. Dajte manji broj zadataka, ali ono sto rade neka rade rucno. Necete dobiti nista od "pameti" ako u medjuvremenu studenti izgube osnove.

Nakon faksa nisam uzeo olovku u ruke dok sestricina nije krenula u srednju skolu. Sada, nakon 15 godina mi je trebalo mesec dana da udjem u fazon integrala i nizova koje sam resavao zmureci.
Sramota je reci da mi je trebalo 2-3 dana da se podsetim osnovne skole i "rastavljanja na proste cinioce" i deljenja brojeva "bez digitrona".

Moja keva je izasla u penziju pre godinu dana kao profesor matematike. Vi koji radite sa brojevima svaki dan, lako se snalazite, ali budite sigurni da sve veoma brzo bledi...
A ja sam se iznenadio koliko je sve izbledelo...

::www.kladovo.net ::

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 20:08 - pre 156 meseci}

zivanicd

A da li ti je smetalo u životu to što nisi znao rastavljanje na činioce ili da računaš integrale na ruke? Ja ne znam čime se baviš, ali očigledno da ti nisu trebali integrali.

Onaj kome trebaju integrali, neka lepo nauči da ih koristi, da prepoznaje šta mu treba u datoj situaciji i kako to da upotrebi. U svakom slučaju mu neće izbledeti znanje koje zaista bude koristio, a za ostalo ionako nema veze.

Naravno, ova priča se ne odnosi na uzrast od 7 do 12 godina, već na fakultete. Pedagoški stručnjaci kažu da u tom periodu treba zadavati probleme koji se rešavaju na cake, ali elementarnim sredstvima, a ne debelim teorijama i koji imaju što jednostavniju formulaciju zbog razvoja saznajnih sposobnosti. No, posle 12 godina mozak je prošao kroz tu fazu razvoja.

Osim toga, nema ama baš nikakve nikakve pameti u računanju kvadratnog korena na ruke. Ko je razumeo numeričku matematiku će to svakako znati da uradi na više načina, ali na vežbama i ispitu ne treba da radi zadatke za zaglupljivanje.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Pitanje o unapređenju nastave matematike

^{16.06.2012. u 20:31 - pre 156 meseci}

Citat:

Nedeljko:
..Ne radi se samo o ispitnim metodama, već i o ciljevima nastave. Dakle, o tome kakvo znanje treba prenositi i šta je to upotrebljivo znanje....

Dosta toga diktiraju globalni trendovi.Nisam upućen,ali pretpostavljam da je razvoj matematike dosta slobodan.Šta će od novih stvari ući u programe nastave,a šta će biti izbačeno ili redukovano,ne znam?
Ali znam ovo:Za razliku od školovanja predavača matematike,studiji na tehničkim naukama moraju se brzo prilagođavati novim tehnikama.
Dobri matematički programi na računarima treba da redukuju uvježbavanje silnih zadataka.Naprimjer ja sam imao integrale cijeli semestar (6+4).To bi sad trebalo ići na pola ili još manje,a umjesto toga nešto korisno.Fakulteti (profesori) su tromi,treba im dosta vremena da se prešaltaju.To treba ubrzati.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.54.*

+64 Profil

Re: Pitanje o unapređenju nastave matematike

^{17.06.2012. u 09:31 - pre 156 meseci}

@bojan

Citat:

Možeš ti i celog semestra dogmatski ponavljati neko trabunjanje o generalnom iskustvu i o korisnosti fore iz tog-i-tog dokaza, ali to neće imati nikakvog efekta (bar ne pozitivnog!) ako se studentu ne predoči potreba za time na nekom živom primeru.

Ne razumem kako si shvatio da ja zelim da se studentima dogmatski ponavlja trabunjanje? :) Stvarno svasta... Ja sam samo rekao da je korisno da zna puno dokaza, jer ih moze kasnije iskoristiti. Isto kao sto mu je korisno da zna da sabira...

Citat:

Nedeljko: Mala varijacija ideje dokaza teoreme jedinosti.

Bas ono o cemu sam pricao.

_{[Ovu poruku je menjao darkosos dana 17.06.2012. u 10:41 GMT+1]}

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.54.*

+64 Profil

Re: Pitanje o unapređenju nastave matematike

^{17.06.2012. u 10:38 - pre 156 meseci}

I da, naravno da se stecenom znanju najbolje daje smisao kroz konkretan problem (ne mora bas zivotni :), jer student tada ima osecaj vrednosti svog znanja. Da ne kazem da se ponavljanjem/koriscenjem utvrdjuje znanje. Ali to je vec drugi problem, koji sada ima veze sa odnosom profesor-asistent (makar je tako bilo u moje vreme). Ovaj ti prica jedno na predavanjima, ovaj ti radi 6te zadatke na vezbama. Ne znam ja i sada mislim da je bilo dobro sto je recimo profesor Linearne Algebre nama drzao i predavanja i vezbe. Mada je mnoge nerviralo to sto je prolazio pored svakog, gledao sta radi, kao u srednjoj skoli :) Ali verujem da se dobar odnos predavanja/vezbe moze napraviti i sa dve (razlicite) osobe :) ako imaju dobru saradnju i slicne poglede na to sta i kako treba da se radi.

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Pitanje o unapređenju nastave matematike

^{26.06.2012. u 00:13 - pre 156 meseci}

Citat:

darkosos:
Ne razumem kako si shvatio da ja zelim da se studentima dogmatski ponavlja trabunjanje? :) Stvarno svasta... Ja sam samo rekao da je korisno da zna puno dokaza, jer ih moze kasnije iskoristiti. Isto kao sto mu je korisno da zna da sabira...

Jesi rekao da je korisno da zna puno dokaza jer ih kasnije može iskoristiti, ali sam stekao utisak da si pod time mislio kako te dokaze treba eksplicitno zahtevati. Pominjao si dva moguća principa rada, koji funkcionišu u zavisnosti od toga za šta treba osposobiti studenta, ali oba tvoja principa počinju sa „ovo ti treba jer...“ Tu se ne slažemo. Moj stav je da ih ni na šta ne treba terati da uče, već ih treba pustiti da oni sami shvate kako bez znanja tih dokaza neće umeti da urade zadatke na ispitu (to jest, ako mu treba „ona ideja iz onog dokaza“, neće imati vremena da na samom ispitu iščita — iako mu je sve dostupno! — sve ideje koje su se pojavljivale na predavanjima/vežbama, kako bi prepoznao onu koja mu u datom momentu može pomoći).

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.static.isp.telekom.rs.

+64 Profil

Re: Pitanje o unapređenju nastave matematike

^{26.06.2012. u 08:48 - pre 156 meseci}

Slazem se da u nasem obrazovanju ima previse teorije na racun prakse... To onda dozvoljava studentu da "nabuba" dokaz, na pismenom uradi sablonske zadatke, i mozda dobije konacno i 10 a da nista pametno nije uradio... Ali i tvoj stav je drastican, sada je klatno u suprotnom ekstremu: nijedan dokaz koji ne moze da se primeni na zadatke. Slazem se, hajde da kazemo, za vecinu dokaza. Kao sto sam napisao u prethodnoj poruci, ovo mora biti dobro sinhronizovano izmedju predavaca i onog ko drzi vezbe, tj. radi zadatke.

Prvo, pitanje je sta je plan i program konkretnog kursa? Dakle sigurno postoji neki "cilj" kursa. Svakako da ljudima sa tehnickih fakulteta treba vise prakse, jer ce resavati konkretne probleme, dakle koristiti matematiku kao alat. Ma mozda im ne treba nista od teorije, sto rece Nedeljko, nek' nauce da koriste neke od brojnih matematickih programa.

Ali mislim da student matematike mora imati i deo teorije koji mozda ne moze da se direktno iskoristi u nekom zadatku. To mogu biti neki zaista bitni dokazi. Ili na primer neki koji sadrze neku sjajnu ideju, koji pokazuju lepotu matematike. Ne mogu da se pomirim sa tim da se sve to izbaci samo zato sto ne moze da se napravi zadatak, ili makar ne takav koji moze da se resi za odgovarajuce vreme. I na kraju krajeva - to se kosi sa onim osnovnim u matematici: ako nesto tvrdis, za to moras da imas dokaz. Pa ako tako gledamo, i na pismenom ispitu se trazi, ne neki nacin (mozda indirektno), dokaz da je rezultat taj i taj. Da li ti prihvatas nesto sto napise student, npr. neku formulu, koja nije standardna vec moze da se izvede na licu mesta, a da nema opravdanja, makar recima, da je to tako? Znaci odjednom samo bubne ovo je ovoliko i cao? Dolazak do resenja je nesto kao dokaz, jer mora da prati pravila izvodjenja. Pa i u zivotu, kad neko nesto kaze, trazis dokaz, argument - kao sto i mi ovde pricamo :). Pa onda jedan argument na drugi, pa provera, trazenje kontraprimera i na kraju se svede na licni osecaj iliti veru :) Salim se sad malo, ali poenta je ovo: covek koji se bavi naukom koja je tako koncipirana da trazi formalna opravdanja, tesko moze da prihvati nesto bez tog opravdanja. Slazem se da moze biti onih koje preskacemo iz prakticnih razloga, pa se kaze studentima: imajte malo vere da je to sve ok. Ali recimo, evo ja licno sam zavoleo teorijsku matematiku bas zato sto se za sve daje dokaz. I tu je mozda mesto razilazenja - ja nisam goal-driven orijentisan; znaci pitanje je afiniteta: manje mi znaci to sto resim problem, nego npr. dolazenje do ideje i mozda uopstavanje - trazenje dometa problema.

Dakle, da rezimiram, tvoj (i Nedeljkov) stav da treba uneti zivota u prosvetu podrzavam u potpunosti. Koliko mi se cini, ti si asistent na nekom fakultetu, pa bas zbog toga sto je potrebno da neko malo razdrma tu ucmalost, cak bih dopustio i tvoj radikalni stav :) A klatno ce vec naci svoju, sto bih ja rekao, dinamicnu ravnotezu :)

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Pitanje o unapređenju nastave matematike

^{26.06.2012. u 10:46 - pre 156 meseci}

Citat:

darkosos: To mogu biti neki zaista bitni dokazi.

Još samo kada bi obrazložio po čemu su ti dokazi bitni.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.static.isp.telekom.rs.

+64 Profil

Re: Pitanje o unapređenju nastave matematike

^{26.06.2012. u 11:05 - pre 156 meseci}

Obrazlozi po cemu nisu :)

EDIT: U stvari, nema sta da obrazlazes. Dokazi u matematici nisu bitni... Profesori su potpuno suvisni, jer bi se na predavanjima samo izlagala veronauka u obliku katahizisa. I onako iskaze teorema mogu studenti da nadju gde bilo.

_{[Ovu poruku je menjao darkosos dana 26.06.2012. u 13:44 GMT+1]}

Odgovor na temu

[es] :: Matematika :: Pitanje o unapređenju nastave matematike

Strane: 1 2 3

[ Pregleda: 7755 | Odgovora: 50 ] > FB > Twit

Srodne teme

21.06.2007. Kako da se nastave sledeci brojevi 1,8,9.... moli..
05.09.2007. Tekstualni zadatci iz matematike
29.03.2008. Seminarski rad iz poslovne matematike
04.12.2009. Deljenje konekcije preko modema ali sa virtualnom..
01.09.2010. Interaktivni web testovi iz matematike
12.10.2010. rjesavanje zadata iz matematike
22.11.2010. Pitanje iz matematike
03.03.2011. literatura knjige iz matematike
24.09.2011. Pocetak nastave na ETF u . POMOC

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.