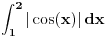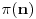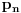Pitanje o unapređenju nastave matematike

Ovo pitanje je pre svega upućeno Bojanu Bašiću, jer delim njegov pogled na nastavu i ispitivanje, a on takođe radi u nastavi. Naravno, svi ostali su takođe pozvani da iznesu svoja mišljenja i doprinesu kvalitetu teme.

Da li bi bilo dobro da na ispitima iz matematike svaki student ima na raspolaganju laptop sa instaliranim matematičkim softverom i enciklopedijama, a koji ne bi bio priključen na internet? Lično ne bih imao ništa protiv ni korišćenja interneta ako se on ne bi koristio za komunikaciju sa drugim licima koja bi krišom učestvovala u izradi zadataka, davanjem ideje ili slanjem kompletnih rešenja, ali to je teško kontrolisati.

---

Naravno, zadaci bi morali da budu odgovarajući, a ne prosta primena formula za koje studenti posle ne znaju šta će im. E, ali onda i nastava treba da bude takva da obučava studente za rešavanje matematičkih i nematematičkih problema matematičkim metodama.

---

Da, to jeste taj problem sto bi se onda neki zadaci mogli resiti bez previse znanja o materiji. Mozda je bolja ideja uradii obrnuto, dati kontrolisan skup informacija na koriscenje. Malo bi bilo nezgodno za matematicki program, kako iskljuciti opcije? Ali, npr. kao u skorasnjoj temi sa "ciklicnim" sistemom, ako imas program, uradis rastavljanje (i odredjivanje nula) pre nego kazes keks. Sa druge strane, zadaci koji traze ideju su npr. 1 ili najvise 2 zadatka na ispitu, makar je tako bilo u moje vreme. Ostalo je prakticno rutina. Dakle spemanje zadataka bi postalo jos nezgodnije, pa bi tako nesto prakticno znacilo revoluciju u obrazovanju (kao sto je to bio digitron :)).

Zamisljam sada ovako nesto: umesto klasicnog matematickog programa, dati nesto kao "jelovnik za racun", gde bi se kontrolisalo sta se pita. Npr. pokrenes program, izaberes od ponudjenih opcija sta zelis da izracunas i posaljes pitanje, dobijes odgovor. Nesto kao matematicki firewall :) A onda onaj ko daje zadatke mora da podesi i firewall. Posto postoje ti command line programi, ovo bi moglo relativno jednostavno da se odradi. Uz ovo bi naravno trebalo da postoji i jelovnik formula.

Poenta je čemu na ispitu zadaci koje računar rešava automatski? Kakva je praktična kmorist od tog znanja? Kakva je korist od znanja dokaza sto kila teorema, pri čemu svaki od tih dokaza piše u svakoj knjizi? Da li je sa pojavom matematičkog softvera prestala potreba za matematikom? Naravno da ne. Praktičan problem je što gro predavača nemaju pojma o značaju onoga što predaju i što ne umeju da prave takve zadatke. Pojavom matematičkog softvera nije prestala potreba za matematikom, nego za takvim matematičarima.

Svojevremeno su na pismenom iz osnova geometrije u Beogradu sva četiri zadatka bila za razmišljanje. Onaj zadatak o ciličnom sistemu jednačina je zahtevao razmišljanje, jer da nije, postavljač teme bi ga samostalno rešio i ništa ne bi pitao. Takođe se zzzz kao pristojan matematičar na ovom forumu okliznuo. Lako je meni bilo da faktorišem polinom korišćenje programa wxMaxima, ali je trebalo doći do tog polinoma i znati šta posle s njim raditi. U tome je stvar, a ne da računam broj pi na sto decimala na ruke.

---

Pa danas racunar zna svasta da resi automatski, nisam siguran da sve to student sme da ne zna... Uostalom, ko ce da pravi dalje te programe pa i samo da odrzava :) Mozes da kazes da npr. posto se rastavljanje na cinioce ozbiljnije radi u srednjoj skoli, da tada ucenik ne sme da koristi pomocna sredstva. A da kasnije, kada mu to zatreba, moze da uradi masina, jer on vec zna kako se radi, a sto da trosi vreme, kad to ionako nije poenta...

Ali ja bih svakako uveo pravilo da u toku skolovanja svaka racunska metoda mora da prodje "kroz ruke" (mozda sa izuzetkom nekih smorova tipa n-ti koren, logaritmi ili slicno - ali svakako metode koje se rade simbolicki). Pa kako postoje metode koje se uce tek na studijama, onda bi to moralo da vazi i za takve metode. E sad, kako ce neko da odvoji sta se podrazumeva da student zna (tj. da je presao to na ruke), a sta je tematika samog kursa? Pa tako sto ce, kao sto sam predlozio, da se napravi spisak sta student moze da uradi pomocu masine a sta ne.

Na kraju krajeva, i samo znanje pesackog tipa mora da se obnavlja. Kao sto si i sam rekao na nekoj temi ovde skoro, mozda bi neko ko pise knjige mogao da napise iz glave, ali nekako je to moralo u tu glavu da stigne. Pa na primer i sam predavac, zar bi mogao da prikaze dokaz necega a da ne prodje kroz detalje, gde ponekad oni takodje zahtevaju dosta osnovnog racuna. Da li prihvatio dokaz koji je uradila masina? Postoji i takav softver. A onda, ako to zahtevamo od predavaca, zasto da ne zahtevamo od studenata. Potpuno se slazem da ne sme "ranije predjeno gradivo" da prevazidje tematiku kursa, ali ovo je nesto drugo. Kao sto si svojevremeno ucio sabiranje kroz puno primera, sredjivanje algebarskih izraza, ucio tablicu mnozenja napamet, tako moras da prodjes i kroz tablicne integrale, standardne tehnike resavanja i puno zadataka "na ruke". Zato da bi kasnije znao i da uradis neki komplikovaniji zadatak - naravno to je samo potreban uslov :)

Taj softver će da piše onaj ko prouči te metode, a to je onaj ko je naučio da misli. Pretpostavljam da si programer u nekom višem programskom jeziku. Ima li leba bez asemblera? Pa, ima. Naravno da prevodioce mora neko da napiše, ali to je radio neko ko sjajno zna asembler. Ne moraju i ne mogu svi znati sve. Stekni nekakva upotrebljiva znanja i koristi ih. To mogu da budu i asembler i teorija prevođenja. OK, i to treba neko da zna.

Sa druge strane, što se prolaska osnovnih metoda na ruke tiče, to može da se pita na usmenom, a na pismenom da se proverava operativno znanje. Na kraju, Bojan Bašić je pominjao neku teoremčinu koja se dokazuje na trocifrenom broju strana i za koju na studijama nema vremena da se izvodi njen dokaz. Da li je to razlog da se ta teorema ne uči i ne primenjuje? Pa, ne. Jednostavno treba reći gde se dokaz može naći, pa ko hoće, neka ga nauči, a na vežbama da se rade primene te teoreme.

---

Pretpostavljam da si mene pomenuo zbog toga što znaš da dozvoljavam korišćenje bilo kakve literature (u papirnom obliku) na kolokvijumu/pismenom ispitu, pa pitaš smatram li da je ovo logičan sledeći korak. Ako bi se ovo što predlažeš moglo u praksi izvesti, apsolutno bih bio za to. No, tako nešto ipak je praktično nemoguće. Prvo, ako bi se omogućio izlaz na internet (za šta takođe smatram da bi bilo u redu — uz, jasno, zabranu komunikacije s drugim licima), bilo bi nemoguće kontrolisati upravo komunikaciju s drugim licima. Drugo, i ako je izlaz na internet onemogućen, opet će se u praksi teško dogoditi da fakultet omogući laptopove svim studentima na svim ispitima. (Što se tiče predmeta koji se polažu na kompjuterima, u računarskim učionicima, to obično biva dosta nezgodno — ispiti traju po više dana, mora se praviti zilion grupa zadataka, i sve to funkcioniše samo zahvaljujući tome što takvih ispita ima dovoljno malo; ako bi se svi ispiti održavali u računarskim učionicama, otišlo bi sve u majčinu.) Varijanta da svaki student donese svoj laptop takođe je neprihvatljiva, počev od toga što se time u startu favorizuju studenti koji imaju laptopove (a nemaju ih svi, niti imaju svi novca da ih kupe), pa nadalje. I najzad, u bilo kom od poslednja dva scenarija, studenti bi mogli prokrijumčariti mobilni internet u amfiteatar (cenim da modem u formi USB stika ne bi bilo previše teško uneti u amfiteatar i krišom ga uštekati u USB port), a time opet puca cela koncepcija.

Dakle, zaključak: teorijski, veoma se slažem s idejom koju si izneo; praktično, ona je neostvariva.


Nažalost, apsolutno si u pravu.

---

Iako poredjenje sa programiranjem ina smisla, ipak prakticno programiranje nije nauka. Mnogo puta napisem nesto i ne razmisljam previse da li je to 100% ok, vec pustim prvo da masina iskompajlira, dakle da prodje sintaksno, pa onda pokrenem da vdim da li radi kako treba, a nerertko se desava i da se mnogo kasnije nadje neki "bug". Ja sam sklon da kazem da je programiranje slicnije zanatu. Pa tako koristim alatke koje su drugi napravili, kao sto nas svih nema, u savremenom drustvu, bez mnogo stvari o kojima ne razmisljamo, npr. da neko negde treba da pozanje, zavari, stisne... To su preduslovi da mi "odemo dalje" i da koristimo stvari kao sto su racunar, internet...

Ali ovde je to sve deo jedne celine, i cak bih rekao da potpomaze napredovanju. Uostalom, nije mi jasno sasvim koja ti je ciljna grupa? Talentovani studenti matematike? Ili svi koji imaju matematiku kao predmet na studijama?

Bojane,

Nisam tebe prozvao samo zbog toga što si naveo, već i zato što se zalažeš za učenje i onih teorema koje se ne mogu dokazivati na predavanjima i njihovu primenu i zbog toga što smo se složili oko toga gde je mesto analitičkom i sintetičkom pristupu u geometriji (rasprava u čuvenom "metodu pogrešne discipline").

Ako se teorijski slažeš, onda bih u vezi praktičnog sprovođenja rekao sledeće: Sve mašine bi morale da budu fakultetske i nijedan student ne bi imao pravo da donese svoju mašinu. To dalje otvara mogućnost da fakultetsko računarsko osoblje izvadi iz hardvera sve komponente koje se mogu koristiti za pristup internetu. Dakle, nema antene za bežični internet, niti USB priključka. Ima DVD čitač, koji bi fakultet koristio za instalaciju softvera, pa student neka na diskovima donese šta god hoće. Štaviše, može se koristiti izmenjeno linuks jezgro bez podrške za umrežavanje.

Problem je cena svih tih laptopova. Ali, hej, koliko ono fakultet uzima keša po studentu, što od studenata, što iz budžeta? Zar je 70 evra za polovnu mašinu, koja bi trajala dve do tri godine veliki izdatak? Takođe, neka svaki student plaća 100 dinara po ispitu za struju koju će da potroši.

E, sad, glavni i ključni problem je nastavni kadar, koji ne zna da smisli drugačije zadatke od

koji u XXI veku ne služe skoro ničemu.


darkosos,

Programiranje je zanat pravljenja programa, a matematika zanat pravljenja teorema i njihova primena. U oba slučaja se koriste prethodni rezultati i prave i ispravljaju bagovi. Naravno da čovečanstvo treba da sačuva sva bitna znanja, ali ja koristim deterdžente nemajući pojma o hemiji, jer to zna neko drugi, a ja znam nešto drugo, što ću da unovčim da bih kupio deterdžent.

---

Posto je poenta pitanja da li se moze na ispitima dozvoliti sva literatura (veliki deo literature je vec digitalizovan) i usput omoguciti dosta simbolickog racuna ja nisam siguran da je ovo prakticno dobra ideja, iako bi teoretski dala dosta dobre rezultate.
Naravno, da bi odgovori bili precizniji trebalo bi imati informaciju da li se radio o osnovnim studijama, masteru ili nesto vise od toga, ali polazim od pretpostavke da se radi o osnovnim studijama.
Kljucni momenat za nastavak diskusije smatram u kriterijumu koji ispitivac postavi za osnovu ispita tj. kako postavlja pismeni zadatak tj. koju tezinu zadataka daje.

Ako je poenta dozvoliti "sve" (osim komunikacije sa drugima na sipitu) a dati takve zadatke da ti ta "sva" literatura moze malo ili nimalo pomoci na ispitu onda nisam siguran da je to OK pristup, cak sta vise to cesto bude "ometajuci faktor" jer se daje lazna sigurnost studentima da ce nesto korisno isceprkati.
Mislim da je osnovni pristup da se definisu znanja koja student treba da usvoji za dati predmet, da se zatim te teme kvalitetno obrade na predavanjima i vezbama i da zatim ispit bude provera usvajanja tih znanja, i prilagodjen vremenu od npr. 4h.
Kvalitet na ispitu treba biti podrzan kvalitetom pre ispita.
Jer u cemu je poenta dati nesto na ispitu sto nije obradjivano na vezbama i predavanjima? Ili biti tako formulisano da student treba uloziti ogroman napor da bi prepoznao i povezao zadatak sa ispita sa obradjenom teorijom i zadacima na predavanjima i vezbom (govorim o npr. zadacima za 6 ili 7).

I tu dolazim do poente zasto ja ne bih dozvoljavao bas sve na ispitu.
Formule, potrebne teoreme i slicne stvari da, ali ne i ostalo.
Naravno, ne podrazumeva sve ovo da svi zadaci budu takve tezine da ako predjete vezbe ladno mozete dobiti 10, ali da to bude dovoljno za barem 6 ili 7.
Za vece ocene, naravno, trebalo bi formirati ostriji kriterijum.

I skoro da mi nikad nije bilo jasno sta profesori (ispitivaci) tacno ocekuju od studenta na ispitima tj. sta to znaci dobiti 10?
Da li je to kompletno savladan program za taj ispit, za odgovarajucim znanjem u pismenom i usmenom delu ili to znaci nesto sire od toga?
Da li to znaci da kada neko uradi 5 zadataka (100%) na ispitu to znaci da on zna sve ili je jednostavno imao inspiraciju, dobar dan ili zadatke koji su mu isli na ruku?
A moje misljenje je da bi trebalo i pismeni ispit imati vise nivoa za studente koji pokazuju dobra znanja i idu na visoku ocenu jer smatram da se sa 5 zadataka ne moze stvoriti bas neka realna slika o znanjima studenta.

Princip neke standardizacije znanja mislim da je vrlo ozbiljno pitanje i deluje mi da se dosta olako prelazi preko njega i da postoji jako velika sarolikost po ovom pitanju i dosta toga je ostavljeno na savesti profesoru, sto je cesto povod za razne zloupotrebe.
Neki imaju ambicije da sto vise nauce studente a neki da od ispita naprave "baba rogu".

Nedeljko, imam utisak da nece biti lako poloziti ispit kod tebe, pa taman im dozvolio i internet

Imali smo jedan takav predmet-vežbe-ispit. Sve se svelo na to da smo koristili gotove programe, koje je asistentkinja pravila namenski za to specifično gradivo (numerička analiza), da smo katkad samo ubacivali podatke u sličan već urađen zadatak na vežbama (dakle, nije nam na raspolaganju bila samo Wolfram Mathematica), vreme za izradu zadataka je bilo knap, kolokvijuma nekoliko... Uđeš, zarumeniš se brzo razmišljajući i radeći, izađeš, zaboraviš i - gotovo.

Kao što bi pri izradi nekih zadataka bilo mnogo udobnije da se mašina bavi determinantama ili sistemima jednačina, moguće je i napraviti dogovor da se na ispitu iz npr. diferencijalnih jednačina pri rešavanju sistema Lagranžovom metodom ne izračunava sve do kraja, jer nije poenta u izračunavanju silnih integrala. U pomenutoj numeričkoj analizi zgodno je iscrtati grafik funkcije i napraviti solidnu ocenu njenog ekstrema, ali ne vidim baš mnogo drugih predmeta gde bi prednost za ispitivača i studente bilo korišćenje računara. Doduše, ja sam "stara garda" i preferiram više one ispite na kojima se dobiju lepi zadaci za razmišljanje, pa kad na kraju dođeš do ideje, osećaj zadovoljstva te još dugo drži.

---

Moje poredjenje sa zanatom je imalo drugaciji smisao - da zanatlija radi svoj posao ne razmisljajuci mnogo zasto i kako nesto radi (naravno da moze i da zna, ali nije neophodno). On zna da ako uradi to ovako - da ce ispasti onako. A vremenom dolazi do iskustva za razne situacije. Ali nema potrebu da napravi teoremu o tome. Taj korak da napravi od poznatog nepoznato se moze zvati izum, ali nije neophodni deo zanatstva. Po meni, zanatski deo matematike je bas taj koji hoces da izbacis.

Lepo je videti kako se javlja sve više učesnika na ovoj temi sa kreativnim i konstruktivnim komentarima.


igorpet

Nije uopšte poenta da se studntima zagorča život na ispitu. "Kuku majko, koliko ih je položilo." Ne. Poenta je da što veći broj ljudi stekne što upotrebljivije znanje. Ako je lako položiti ispit, onda postoji problem, ali ne u tome što je masa položila, već u tome što se sa razumnom težinom moglo naučiti više. Dakle, otežaj ispit proširivanjem sadržaja, a ne teranjem studenata da drndaju determinante i faktorizaciju polinoma u ekstremno kratkom vremenskom roku.


darkosos

Zanatljija mora da napravi bravu koja radi. Ako on ne zna šta treba da zna u vezi pravljenja pumpi, neće moći ni da je napravi. Isto je i sa pravljenjem teorema. Kao što obućar ne mora da razume međumolekularne sile da bi nešto zalepio, već samo da zna kako to da uradi, tako i matematičar istraživač treba da zna samo koja mu teorema treba i kako tačno glasi, a ne i njen dokaz.

Svojevremeno nam je asistent iz verovatnoće i statistike zadao zadatak koji je ekvivalentan velikoj Fermaovoj teoremi. OK, neko je dokazao tu teoremu i dokaz je proverio veliki broj stručnjaka iz oblasti. Dakle, tvrđenje je tačno. Treba li zbog toga što ne znam dokaz velike Fermaove teoreme da je ne primenjujem?

---

darkosos

Evo ti jednog konkretnog primera. RSA algoritam je zasnovan na težini faktorizacije prirodnih brojeva. Najjednostavniji algoritmi faktorizacije su eksponencijalne složenosti u odnosu na broj cifara ulaza, ali postoje napredni koji su subeksponencijalne složenosti (ali ne i polinomijalne). No, oni su jako složeni. Da bi studenti računarstva mogli da izračunaju koliki si potrebni računarski resursi za razbijanje RSA sa nekim brojem bitova širine, oni moraju znati složenost problema faktorizacije prirodnih brojeva. Da li to znači da to od njih treba kriti kao zmija noge, jer zaboga, materija je kompleksna da bi se izložila sa dokazima iako je potrebna formulacija dovoljna za račun sasvim jednostavna?

---

Zapravo, ovde se mora poći od toga šta je cilj nastave, pa onda prema svecu i tropar. Ja sam tako razmišljao.

---

Trudimo se da budemo konkstruktivni, a ono sto se meni licno svidja u zadnje vreme na forumu je nivo diskusija, koje su po meni, dostigli jedan pristojan akademski nivo.

A sto se tice "dizanja kriterijuma", pa sad to zavisi od predvidjenog plana i programa rada i ja nisam da se to radi u zavisnosti od prolaznosti.
U stvari najbolje bi bilo kad bi realno steceno znanje omogucavalo da student polozi ispit u nekom razumnom roku (2-3 ispitna roka) i to bi, prema meni, znacilo visok nivo kvaliteta vezbi i predavanja i motivisanosti studenata a ne nesto trece.
A "dizanje nivoa" trebalo bi da se odnosi i na kvalitet nastave i da to bude u srazmeri i tada bi po meni bilo OK.

A ako poenta zadatka nije npr. determinanta ili prost racun, faktorizacija ili nesto slicno dovoljno je omoguciti studentima one malo naprednije digitrone ili eventrualno u dozvoljenim formulama navesti primere resenja 10-ak determinanti ili neke faktorizacije koje mogu biti deo nekog zadatka i time dati gotova resenja tog dela zadatka. Da ne bi to licilo na navodjenje do resenja celog zadatka onda dati malo veci broj mogucih i slicnih resenja.
Mozda dozvoliti kompletan laptop sa svim i svacim, zbog samo ove namere, bi bilo isuvise.

I po mom misljenji i kad resimo da dozvolimo i kad resimo da ne dozvolimo nesto to mora imati svoj smisao tj. moramo tacno znati zasto i sa kojom namerom smo nesto dozvolili ili nismo dozvolili. Pedagoski pristup i korektnost se ne moze nauciti tek tako kao neki ispit, covek ili ima osecaj za tako nesto ili nema, otprilike nesto kao i talenat.

I kao sto si napomenuo, kad znamo sta je cilj nastave i definisemo plan, udarimo po kriterijumima pa onda muski po tabli i tek na kraju po studentima. Obrnuto bi bilo potpuno nekorektno.

Ok, to je cini mi se nesto drugo. Pitanje je da li je dozvoljeno izloziti teoremu bez dokaza? Pa slozio bi se da je to ok, zaista je besmisleno, posebno ako je nesto korisno, a radi se o prevelikom dokazu. U izlozenom slucaju, sudent racunarstva koristi rezultate druge grane matematike. Pa, sto se mene tice, student racunarstva ne mora da zna nijedan dokaz :) Mislim, za sta mi osposobljavamo tog coveka? Da dokazuje teoreme ili da pravi programe? A student teorijske matematike? Pa on bi valjda trebao da zna vecinu, to mu je zanat... Ne zato sto ce mu znaciti dokazi da bi izveo iz njih nesto drugo, nego bas zato da bi stekao generalno iskustvo, koje ce mu pomoci da sam dodje do ideje za nesto drugo. Moze da mu padne na pamet: hej pa ovde mogu da iskoristim foru iz tog i tog dokaza...

Mislim, generalno ja jesam za taj pristup: ok, cime ces da se bavis? aha, pa onda treba da prodjes ovo. I dva principa: 1. ovo ti treba jer ti treba; 2. ovo ti treba jer razvija sposobnosti koje ce ti pomoci.

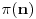
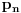
Nisam siguran na koju konkretno misliš da sam je pominjao, ali ima više takvih primera. Iz teorije brojeva tu spadaju, recimo, teorema Erdeša i Selfridža (da proizvod nekoliko uzastopnih prirodnih brojeva ne može biti potpun stepen), asimptotska procena za i , Bertranov postulat, Dirihleova teorema o prostim brojevima u aritmetičkoj progresiji, teorema Grina i Taoa o prostim brojevima u aritmetičkoj progresiji, tehnika rešavanja Pelovih jednačina preko verižnih razlomaka, velika Fermaova teorema (što mi je omiljeno od nabrojanih stvari), i možda još neka dva-tri primera kojih se trenutno ne mogu setiti. Iz geometrije ima (očekivano) dosta manje sličnih primera, ali i tu recimo ne dokazujem da svaka poligonalna linija (bez tačaka samopresecanja) deli ravan na tačno dve oblasti, od kojih je tačno jedna ograničena; kažem studentima da to uzmu kao takvo (i u ovom slučaju stvarno nemaju problema da mi poveruju, jedino imaju problema da shvate zašto ja uopšte pričam bilo šta o tome, kad je to „očigledno“ :)). Pritom, ovde sam navodio samo stvari koje se pominju bilo na predavanjima, bilo na vežbama (a uglavnom na oba mesta), i za koje, imajući to u vidu, smatram da imam pravo tražiti ih na kolokvijumu/pismenom ispitu (primenu, ne dokaz). Činjenica da sam ovde nabrojao, dakle, samo stvari koje se pominju na nastavi, ne isključuje mogućnost da student uradi neki zadatak na drugi način od onog koji sam zamislio (pri čemu se moje zamišljeno rešenje oslanja, naravno, isključivo na gradivo s predavanja/vežbi), i da tom prilikom iskoristi neku teoremu koja nije pomenuta tokom nastave (moguće i neku čiji dokaz zauzima trocifren broj strana); u tom slučaju dobio bi maksimalan broj bodova, pod uslovom da me uveri da stvarno zna da je takva teorema dokazana u literaturi (dakle: ako teorema ima neko ime, može je navesti po imenu; ako pak nema ime, može navesti referencu gde se ona može pronaći).

Još jedna stvar koju takođe aktivno pominjem jesu problemi koji su trenutno otvoreni. Drugim rečima, na vežbama i kolokvijumima viđeni su zadaci tipa „pod pretpostavkom da važi Goldbahova hipoteza, dokazati...“, ili „naći vrednost tog-i-tog parametra takvu da ta-i-ta hipoteza (formulisana u zavisnosti od dotičnog parametra) bude ekvivalentna hipotezi o prostim blizancima“. Smatram da je dobro praviti ovakve konekcije sa savremenim tokovima teorije brojeva (jasno, u onolikoj meri koliku dopušta nivo predmeta na osnovnim studijama).


Imao sam u glavi nešto veće svote za jedan takav laptop, i prilično sam iznenađen tvojom tvrdnjom da je 70 € dovoljno (no nema potrebe da navodiš dokaze, verujem ti, samo prosto nisam očekivao). No, ako uzmemo da bi trebalo nabaviti recimo 100 komada takvih laptopova, to onda izađe 7000 €, što je opet svota koja nije basnoslovna za fakultet, ali ja prosto nemam osnova da od fakulteta tražim tih 7000 € samo za sebe i svoje ispite (primeti da — budući da sam, koliko mi je poznato, jedini koji sprovodi čak i ovu praksu s papirnom literaturom — možemo uzeti kao izvesno da niko osim mene ni te laptopove neće koristiti). (Da napomenem još i to da nisam nikada imao problema s rukovodstvom šta god sam tražio da se nabavi za nastavu i sl., ali je verovatno fazon upravo u tome što, kad god sam mislio da bi nešto bilo dobro da se nabavi, prvo sam procenio koliko je to smisleno tražiti; ovo nikako nije smisleno, bar dok je raspodela stavova povodom korišćenja literature na ispitima ovakva kakva je trenutno.)


A kako tačno misliš da se odredi šta je „potrebno“? :) Nešto tipa da predmetni profesor na nekoliko stranica napravi kompilaciju onoga što je „potrebno“, to podeli studentima, i kaže da smeju kod sebe imati te papire i ništa više? Može, u teoriji izgleda lepo, ali u praksi ruku u vatru stavljam da će se naći bar jedan student kome će smetati što baš te-i-te formule/teoreme nema na papirima (znači, bukvalno šta god da na njima piše, nekome će nešto zafaliti :)). Nije li zato jednostavnije dozvoliti da svako sebi proceni šta će mu trebati, i to i ponese?


Taman posla, naopako bilo da se da nešto što nije obrađivano, ili da formulacija bude namerno iskomplikovana. A što se tiče lažne sigurnosti, poenta je upravo u tome da ne treba nositi od literature nešto u čemu ne znaš šta piše, u nadi da ćeš se na licu mesta upoznati s teoremama odatle, u slučaju da ti zatrebaju (!). Takav pristup osuđen je na propast, i (žao mi je što to moram ovako grubo reći): ako neko padne dva-tri puta, a i dalje ne uspeva da ukapira kako mu je totalno pogrešna koncepcija da na samom ispitu lista nešto što prethodno nije prelistao kod kuće — onda je sam kriv što je postao žrtva te pomenute lažne sigurnosti. I mogu ti reći da studenti koje tokom nastave zapazim kao dobre najčešće ili na ispit ne nose apsolutno ništa, ili eventualno ponesu svoju svesku s vežbi, da im se nađe za svaki slučaj.

A uzmimo sada da je neko čitao i neku literaturu sa strane, u želji da produbi znanje stečeno tokom nastave, pa je pronašao neke teoreme za koje mu se čini da bi možda mogle „jeftinije“ rešiti neke zadatke iz određene tematike obrađivane na predavanjima i vežbama, no nema vremena/volje/želje da pamti sve te teoreme koje je pronašao, da pamti sve uslove koji moraju biti ispunjeni da bi se neka od tih teorema primenjivala i sl. Treba li njega obeshrabrivati povodom takvog vida produbljivanja znanja? Pa jasno da ne (čak upravo suprotno!). Njemu treba omogućiti da, ako zna da postoji „neka slična“ teorema, onda može na licu mesta proveriti kako tačno glasi i da li mu stvarno može pomoći u dotičnoj situaciji. A ako neko nema blage veze šta sve postoji u nekoj knjižurini za koju mu je kolegin kolega rekao da „u njoj ima sve“, pa očekuje da će na licu mesta pronaći nešto što se može iskoristiti — e jbg., nadamo se da će brzo shvatiti da tako ne ide.


Slažem se samo delimično. Tačno je da taj tvoj student treba da stekne to generalno iskustvo, treba da bude u stanju da se seti fore iz tog-i-tog dokaza — ali potreba za time mora mu se demonstrirati upravo kroz žive zadatke, da se on lično uveri kako fora iz tog-i-tog dokaza može biti korisna i na nekom drugom mestu. Možeš ti i celog semestra dogmatski ponavljati neko trabunjanje o generalnom iskustvu i o korisnosti fore iz tog-i-tog dokaza, ali to neće imati nikakvog efekta (bar ne pozitivnog!) ako se studentu ne predoči potreba za time na nekom živom primeru. A pritom postoje stvari koje zaista nisu predviđene da se ikada u životu uče napamet (tipa, neki izrazito tehnički uslovi neke teoreme), koje će čak i najbolji studenti zaboraviti onog momenta izađu iz amfiteatra (i kada im u nekom momentu života, u istraživačkoj karijeri, zatrebaju ti uslovi, najprirodnije će otvoriti knjigu i proveriti kako tačno glase), a tokom tri sata trajanja ispita biće koncentrisaniji na to da im iz glava ne ispari kako glase dotični uslovi, umesto da mogu svu koncentraciju uložiti na rešavanje zadataka. Ne mislim da je to pravi način rada.

---

Pa otprilike tako nekako. A kompilacija moze imati onoliko strana koliko se smatra da je potrebno. Profesori obicno napisu i svoju knjigu u kojoj bi po prirodi stvari trebalo da bude ono sto treba na ispitu. Na kraju a ko moze bolje od ispitivaca da zna sta ce to pasti na ispitu pa shodno tome on najbolje i zna sta treba staviti u kompilaciju a da ona bude stvarno od koristi. A nezadovoljnih uvek je bilo i uvek ce biti ...

Kada sam mislio na ogranicavanje literature vise sam mislio na zadatke radjene na vezbama i predavanjima jer bi po nekoj mojoj logici barem 1 ili 2 zadatka trebala biti dosta slicna sa onim sto je u tim materijalima pa ne bi bilo fer da neko ponese to i uz malo srece "ubode" nesto sto je blizu 6-ice, kada govorimo o pismenom delu ispita.

Ali, ako pricamo o neogranicenom koriscenju literature na ispitima mozda je interesantniji deo koji se desava ili ce se desiti kada i kod nas sire zazivi sistem "obrazovanja na daljinu" u odnosu na klasicni sistem, i tada "moj sistem" rezonovanja kriterijuma za ispit pada u vodu.
Neki univerziteti u svetu vec imaju u ponudi ovakav sistem obrazovanja, i nisam upoznat sa detaljima da li je tako dobijena diploma ravnopravna ali ogranicenja u tom sistemu mogu biti daleko manje restriktivna nego u klasicnom sistemu gde ipak mozemo imati jak stepen kontrole.

Mozda s ovim pitanjima sirim temu suvise ali smatram da se koncepti vezani za ispite mogu uspesno koristiti u oba sistema.
Bolje je biti pripremljen na tranziciju nego zatecen
Jedino ostaje veliko pitanje da li smo kao rezultat ispita dobili, u sistemu obrazovanja na daljinu, znanje pojedinca ili grupe i da li je to individualna ili grupna diploma

U svakom slucaju o ovome se treba pisati, treba diskutovati, skupljti prakticna iskustva jer ce sigurno biti dobrih, a verovatno jos vise losih predloga, ali iz svega se sigurno moze dobiti neki pozitivan rezultat. Mogucnosti komunikacija, sistemi ali i nacin i tempo zivota su dostigli nivo kada ce u bliskoj buducnosti obrazovanje na daljinu verovatno biti neminovnost. I verovatno nam buducnost donosi manje apsolutnog znanja pojedinca a vise ucenje nacina da se iskoriste mrezni i softverski resursi za dolazenje do resenja.

igorpet

Što se tiče zadatka koji su jako slični zadatku koji je rađen na vežbama, na taj način se na ispitu proverava (skoro) neupotrebljivo znanje, osim ako je taj zadatak nešto što će se posle studija tipičo pojavljivati. Dakle, Bojan i ja zastupamo stav o prenošenju i traženju upotrebljivog znanja.

Na kraju, u tom slučaju bi izrada zadataka bila brža, pa bi student tokom četiri sata mogao da uradi veći broj zadataka, što otvara mogućnost za bolje pokrivanje gradiva zadacima.


Bojane,

Mislim da se stone zadovoljavajuće mašine mogu nabaviti po toj ceni, ali nisam sasvim siguran, jer me takve mašine odavno ne zanimaju. Već skoro pet godina nemam stoni računar. Za sebe kupujem isključivo nove laptopove u rangu cene od oko 500 evra u trenutku kupovine i u tom periodu sam kupio već tri za sebe. No, imam prijatelja koji valja polovnu robu i pouzdano znam da je tržišna cena zadovoljavajućeg laptopa za pokretanje velike većine programa (isključuju se programi kao što su AutoCAD i Photoshop, koje takođe mogu da pokrenu, ali ne na nivou profesionalne upotrebe, a igranje najnovijih hitova je potpuno nemoguće) u naredne dve do tri godine iznosi 100 evra.

No, nisam ja ni mislio da sad tebe naložim da zapucaš u dekanat, već da se razgovara o ovakvoj ideji koliko je dobra, da se širi ako je dobra, pa ako se jednog dana formira kritična masa koja je prihvata, zašto da ne. Međutim, fundamentalan problem su predavači koji svoj predmet ne znaju dovoljno dobro, tj. koji uglavnom znaju da izračunaju samo ono što može i mašina.

Jedan poznanik koji je završio ETF u BG mi je pričao o svom ispitu iz elektronike kod čuvenog profesora Caje. Ispit je bio noćna mora zato što u Cajinom udžbeniku nema skoro ničega opšteg, nego gomile rešenih primera, pri čemu se ideje rešenja ne mogu primeniti nigde drugde ili nije jasno gde i kako. Na stranu što ima i dosta grešaka, za koje ne smatram da treba da budu nepremostiv problem. Onda je našao neku američku knjigu u kojoj je objašnjeno kako se rešavaju zadaci iz elektronike i gle, položio je ispit kod Caje, a da ga nije ni osetio. A dotle, svaki ispitno rok, nauka bato. E, u tome je problem.

---