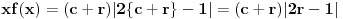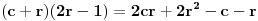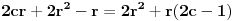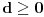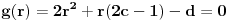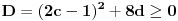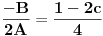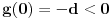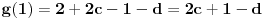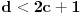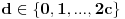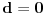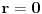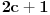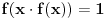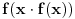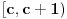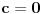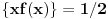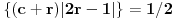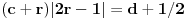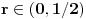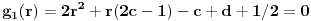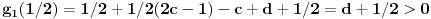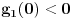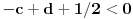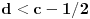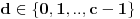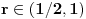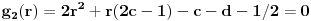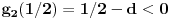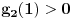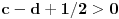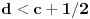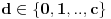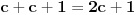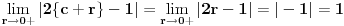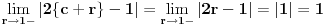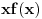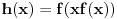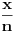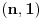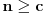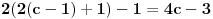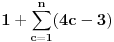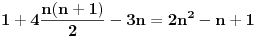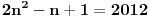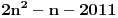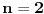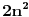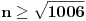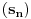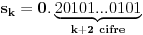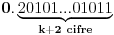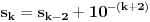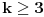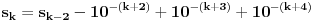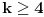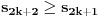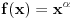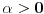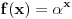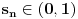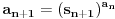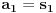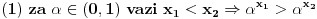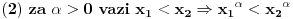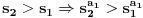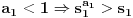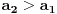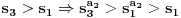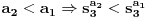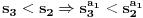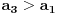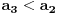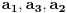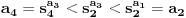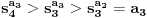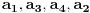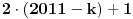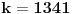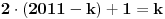Nisam bas sve detalje razradio kako bih zeleo, ali evo:
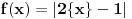
je neprekidna jer je
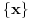
inace neprekidna na svim intervalima (c,c+1) za cele brojeve c, a posto je
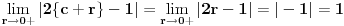
kao i
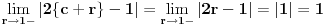
, ova funkcija lepo spaja levi i desni kraj na takvim intervalima. Odavde naravno sledi i da je
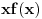
neprekidna, pa je koancno takva i
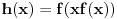
kao kompozicija dve neprekidne.
Pa, ako su prethodna razmatranja tacna, na intervalima
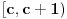
funkcija h(x) dostize 2c+1 puta vrednost 0 i isto toliko puta vrednost 1. Ima jedna sitnica, trebalo bi pokazati da izmedju svake dve nule ima jedan kec, da bi funkcija zaista isla cik-cak, ali nesto me to mrzucka sada... Takodje, treba razmrsiti sta se dogadja u intervalu (0,1), posto tu ima i jedan lokalni minimum koji nije 0, ali i to cu preskociti...
Posto
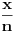
tacno pogadja tacku
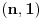
, koja pripada i grafiku funkcije h(x), da probamo da prebrojimo broj preseka za neko dato n, grafika funkcije x/n i h(x). U intervalu [c-1,c), za
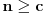
, x/n sece
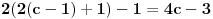
puta (uzeo sam c-1 jer se onda kraj poslednjeg intervala poklapa sa n). Racunajuci i poslednju tacku, (n,1), ukupan broj preseka je
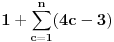
a to je dalje jednako
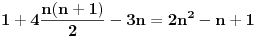
. Dakle, posle svega ovoga, treba jos resiti jednacinu
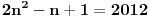
, tj naci najamanje n za koje se dostize vrednost jednaka ili veca od 2012. Pozitivno resenje ove jednacine je priblizno 31.96, a kako je tu funkcija
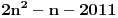
rastuca, moj konacan odgovor je 32, gde bi imali 2017 preseka.
Ako sam i negde oman'o, vec ce neko ispraviti, ali mislim da sam na pravom putu.
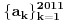 niz realnih brojeva definisanih sa
niz realnih brojeva definisanih sa 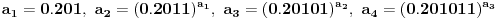 , tj.
, tj.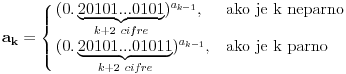
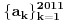 tako da dobijemo opadajuci niz
tako da dobijemo opadajuci niz 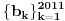 . Kolika je suma svih celih brojeva
. Kolika je suma svih celih brojeva  ,
, 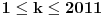 , takvih da je
, takvih da je  ?
?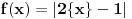 , gde
, gde 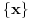 predstavlja razlomljeni deo broja
predstavlja razlomljeni deo broja  . Broj
. Broj  je najmanji ceo pozitivan broj takav da jednacina
je najmanji ceo pozitivan broj takav da jednacina 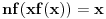 ima bar 2012 realnih resenja
ima bar 2012 realnih resenja  . Koliko je
. Koliko je  ?
? je realan broj
je realan broj 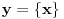 takav da je
takav da je  i
i 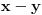 je ceo broj.
je ceo broj.



 Nekoliko random zadataka
Nekoliko random zadataka