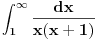Patkane, ovo je integral racionalne funkcije.
Kako se radi?
Imaš integral
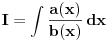
.
1. Izračunaš NZD od brojioca i imenioca, pa ako dobiješ nešto stepena najmanje jedan, skratiš sa tim. Time je problem sveden na slučaj integrala količnika uzajamno prostih polinoma. Stoga ćemo nadalje pretpostaviti da su
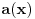
i
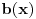
uzajamno prosti polinomi.
2. Podeliš euklidski brojilac sa imeniocem. Dakle, neka je
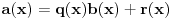
, gde je
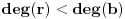
. U tom slučaju je
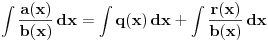
. Integral polinoma pretpostavljam da znaš da računaš (sabirak po sabirak). Time je problem sveden na računanje integrala količnika uzajamno prostih polinoma, gde je deljenik manjeg stepena od delioca.
3. Rastaviš delilac na proste činioce. Dakle,
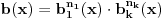
, gde su

prosti i uzajamno prosti polinomi stepena bar jedan.
4. Predstaviš racionalnu funkciju kao zbir sabiraka sa neodređenim koeficijentima na sledeći način: Činiocu
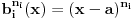
odgovara niz sabiraka
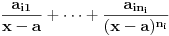
, a činiocu
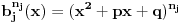
, gde je
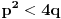
niz sabiraka
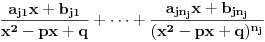
.
5. Kad si to tako rastavio, onda odrediš neodređene koeficijente u brojiocima tako što obe strane pomnožiš sa imeniocem, pa izmnožiš sve i izjednačiš koeficijente uz iste stepene i dobićeš sistem linearnih jednačina po neodređenim koeficijentima sa jedinstvenim rešenjem.
6. Na kraju integrališ sve jedno po jedno. Imaj u vidu smenu
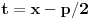
kod imenioca koji su stepeni od
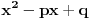
. Takođe, integral
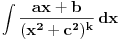
se smenom
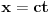
svodi na integral oblika
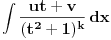
. Dalje je
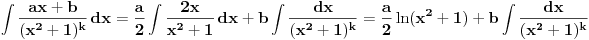
.
Kako na kraju integraliti
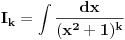
za
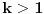
? Parcijalnom integracijom dobijamo da je
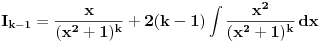
,
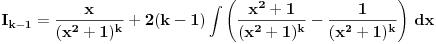
,
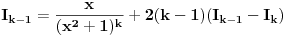
,
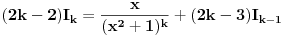
,
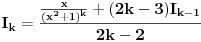
.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.