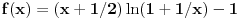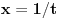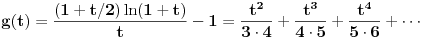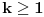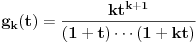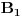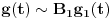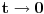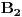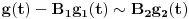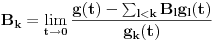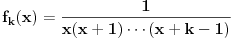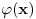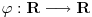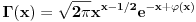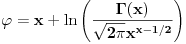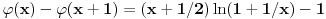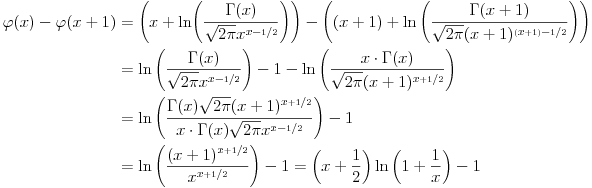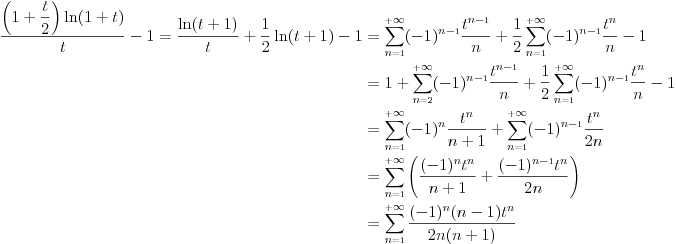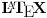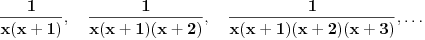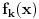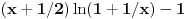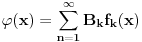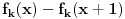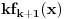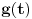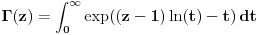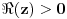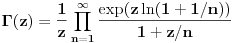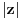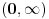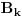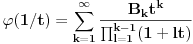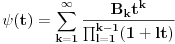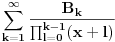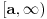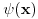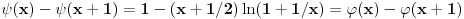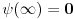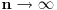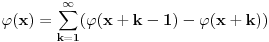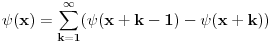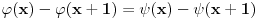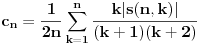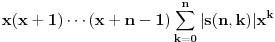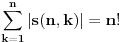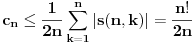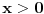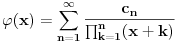Odakle funkcija
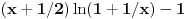
? Pa,
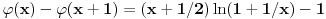
.
Ako je
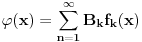
, koliko je
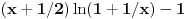
? Koliko je
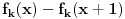
? Da nije možda
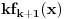
?
Što se ratvoja funkcije
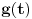
tiče, dobar ti je, ja sam pogrešio.
Što se tiče konvergencije, važi sledeće:
Funkcija
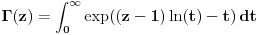
, za
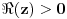
je analitička (na navedenom domenu) jer je granična vrednost lokalno ravnomerno konvergentnog niza analitičkih funkcija. Na primer,
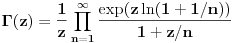
.
Štaviše, gama funkcija je analitička u celoj kompleksnoj ravni bez nepozitivnih celih tačaka. Stoga njen Tejlorov razvoj u okolini tačke

,
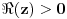
konvergira na otvorenom disku poluprečnika

(pa i više, na disku poluprečnika
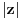
). Otuda je i realna varijanta gama funkcije analitička na intervalu
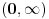
.
Koeficijenti
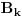
se mogu izraziti preko Stirlingovih brojeva, koji su dobro proučeni, pa se na osnovu njihove procene može dokazati (valjda, nisam računao, ali tako bih probao) da je pomenuti red lokalno ravnomerno konvergentan (u kompleksnoj poluravni desno od imaginarne ose), pa pošto su svi članovi analitičke funkcije i suma je analitička funkcija.
Nakon toga uvedi smenu
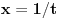
. Zajedno sa funkcijom
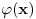
, funkcija

je meromorfna sa otklonjivim singularitetom u nuli (upravo po Stirlingovoj formuli je

). Dakle, treba dokazati da je
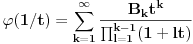
,
pri čemu opet imamo posla sa jednakošću dveju analitičkih funkcija. Dovoljno je dokazati da imaju jednake Maklorinove razvoje. No, to sledi iz činjenice da za
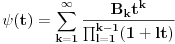
važi

.
Ovako bih ja pokušao da dokažem.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
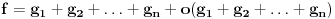 (jer onde kako si zapisao, ne vidim koji je pretposlednji clan (a i deo kod malog o bi trebalo prepravititi (u opstem slucaju))) jer vazi
(jer onde kako si zapisao, ne vidim koji je pretposlednji clan (a i deo kod malog o bi trebalo prepravititi (u opstem slucaju))) jer vazi 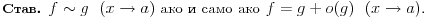




 Re: čika Stirlinge...
Re: čika Stirlinge...