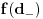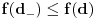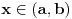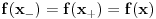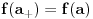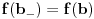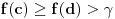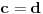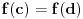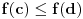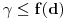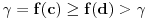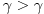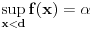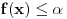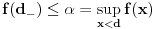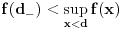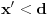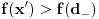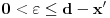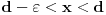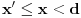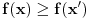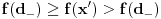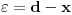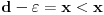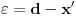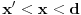Neka je
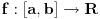 monotona funkcija (realne promenljive) i neka za svaku tačku
monotona funkcija (realne promenljive) i neka za svaku tačku 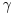 koja je između vrednosti
koja je između vrednosti 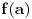 i
i 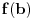 postoji vrednost
postoji vrednost 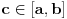 takva da je
takva da je 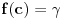 . Tada je funkcija f neprekidna na
. Tada je funkcija f neprekidna na 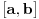 .
.Dokaz.
Pretpostavimo, suprotno tvrđenju, da je funkcija f sa opisanim svojstvima prekidna u nekoj tački
 . Pretpostavimo da je f npr. rastuća i da je, na primer,
. Pretpostavimo da je f npr. rastuća i da je, na primer, 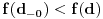 . Ako izaberemo proizvoljno
. Ako izaberemo proizvoljno 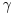 iz intervala
iz intervala 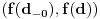 , dobićemo, s jedne strane, da je
, dobićemo, s jedne strane, da je 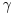 tačka između f(a) i f(b), a s druge strane da
tačka između f(a) i f(b), a s druge strane da 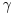 očigledno ne može biti slika nijedne vrednosti
očigledno ne može biti slika nijedne vrednosti 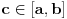 . Ova kontradikcija dokazuje tvrđenje stava.
. Ova kontradikcija dokazuje tvrđenje stava.(Matematička analiza I, Adnađević, Kadelburg)
1. Da li
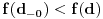 sledi iz toga sto smo pretpostavili da je funkcija rastuća?
sledi iz toga sto smo pretpostavili da je funkcija rastuća?2. Zašto je očigledno?
Hvala unapred!
[Ovu poruku je menjao pitomir dana 18.02.2012. u 11:00 GMT+1]




 Stav o neprekidnosti monotonih funkcija
Stav o neprekidnosti monotonih funkcija