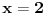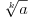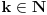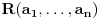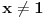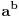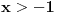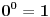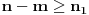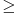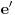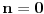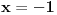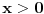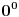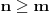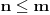Pišem neki članak o dokazima iracionalnosti, koji bi se mogao pratiti sa gimnazijskim znanjem matematike i koji bih okačio negde na internet, kako bi se ovo znanje popularisalo.
Predznanje koje očekujem od čitaoca su osnovne osobine deljivosti (uključujući osobine uzajamno prostih brojeva i teoremu o euklidskom delenju), osnovne osobine limesa, izvoda i integrala.
Za sada sam napisao zajedno sa dokazima potrebnih pomoćnih stavova
1. Potreban i dovoljan uslov da je broj

iracionalan, gde su

i

pozitivni racionalni brojevi i

.
2. Potreban i dovoljan uslov da je broj
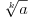
iracionalan, kde je
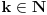
i

pozitivan racionalan broj.
3. Metod za dokazivanje iracionalnosti brojeva kao što su

.
4. Iracionalnost broja

kao i brojeva oblika
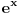
za

, odnosno brojeva

gde je

pozitivan racionalan broj različit od 1.
5. Iracionalnost broja
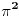
i samim tim broja

.
6. Iracionalnost kvadrata trigonometrijskih funkcija za vrednosti argumenata koje su racionaljne i različite od nule i inverznih trigonometrijskih funkcija za vrednosti argumenata čiji su kvadrati racionalni brojevi različiti od nule.
7. Isto kao pod 6, samo za hiperboličke i inverzne hiperboličke funkcije.
Planiram da dodam:
8. Osobine racionalnih i iracionalnih brojeva kao što su (ne)periodičnost decimalnog zapisa, (bes)konačnost verižnog razvoja i teorema da ako je

proizvoljna racionalna funkcija sa racionalnim koeficijentima i
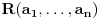
iracionalan broj, onda je bar jedan od brojeva

iracionalan.
9. Veza između funkcija i njihovih inverza. Primera radi, stavovi da su brojevi oblika
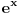
za

i

za pozitivno racionalno
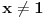
su ekvivalentni.
10. Uopštenje tačke 2 na brojeve oblika
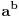
gde su

i

racionalni brojevi.
11. Dopunu tačke 3 do metoda kojim se za svaki broj koji je izražen proizvoljno složenim konačnim izrazom u kome učestvuju celobrojne konstante i operacije sabiranja, oduzimanja, množenja delenja i korenovanja proizvoljnog stepena u konačnom broju koraka utvrđuje da li jeracionalan (i ako jeste koji) ili iracionalan. Postupak bi bio uopšten i na izraze u kojima se pojavljuju konstante koje su algebarski brojevi dati polinomima koji ih poništavaju i lokalizacijama (kojima se razlikuju od ostalih korena).
12. Pojmovima algebarskih i transcedentnih brojeva i osobinama kao na primer da algebarski brojevi čine polje i da su zatvoreni za korenovanje, a transcedentni za stepenovanje i korenovanje, kao i sabiranje, oduzimanje, množenje i delenje algebarskim brojevima različitim od nule. Pojam algebarski nezavisnog skupa brojeva.
13. Konstrukcija transcedentnih brojeva Kantorovim dijagonalnim postupkom i beskonačnih algebarski nezavisnih skupova istom metodom.
14. Liuvilova teorema i opšti postupak konstrukcije transcedentnih brojeva njenom primenom.
15. Transcedentnost broja

.
16. Lindemanova teorema i Lindeman-Vajerštrasova teorema bez dokaza i posledice. Skica veze sa nemogućnošću kvadrature kruga lenjirom i šestarom.
17. Geljfand-Šnajderova teorema bez dokaza i posledice.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
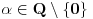 , onda
, onda  . Isto pitanje važi i za teoremu da je
. Isto pitanje važi i za teoremu da je 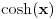 iracionalan broj za
iracionalan broj za  . Oboje svakako sledi iz Lindemanove teoreme da je
. Oboje svakako sledi iz Lindemanove teoreme da je 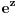 transcedentan broj za ma koji algebarski broj
transcedentan broj za ma koji algebarski broj  , koju je Lindeman dokazao 1882, a da li je bilo poznato ranije? Takođe me zanima da li su sledeći podaci o ljudima koji su prvi dokazali navedene teoreme tačni:
, koju je Lindeman dokazao 1882, a da li je bilo poznato ranije? Takođe me zanima da li su sledeći podaci o ljudima koji su prvi dokazali navedene teoreme tačni: je iracionalan - Ojler,
je iracionalan - Ojler, je
je 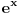 iracionalan - Ojler,
iracionalan - Ojler, je iracionalan - Lambert,
je iracionalan - Lambert,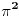 je iracionalan - Ermit.
je iracionalan - Ermit.



 Istorija dokaza iracionalnosti
Istorija dokaza iracionalnosti