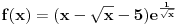Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.

Muke sa asimtotama

[es] :: Matematika :: Muke sa asimtotama

Strane: 1 2 3

[ Pregleda: 8446 | Odgovora: 44 ] > FB > Twit

Postavi temu Odgovori

Autor
Pretraga teme: Traži
Markiranje Štampanje RSS

devetkamp
Dusan Mijajlovic
PMF- Nis, MATEMATIKA - I godina
Prokuplje

Član broj: 293179
Poruke: 113
*.dynamic.isp.telekom.rs.



+1 Profil

icon Re: Muke sa asimtotama28.12.2011. u 14:21 - pre 162 meseci
A sta je sa ovom? Ona je neprekidna, i cini mi se ima vertikalnu.
 
Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.dynamic.isp.telekom.rs.



+64 Profil

icon Re: Muke sa asimtotama28.12.2011. u 14:29 - pre 162 meseci
http://www.elitesecurity.org/t...je-vezi-neprekidnosti-funkcija
 
Odgovor na temu

SrdjanR271
Srdjan Radosavljevic
dipl. inženjer informatike

Član broj: 174403
Poruke: 443
*.adsl.eunet.rs.



+88 Profil

icon Re: Muke sa asimtotama28.12.2011. u 17:46 - pre 162 meseci
Ima prekid u nuli.
A mathematician is a blind man in a dark room looking for a black cat which isn't there.
 
Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.



+2801 Profil

icon Re: Muke sa asimtotama28.12.2011. u 18:12 - pre 162 meseci
Izvinjavam se, ali moram da intervenišem.

Neprekidnost funkcije se definiše samo na domenu funkcije. U tačkama u kojima funkcija nije definisana ona nije ni neprekidna ni prekidna. Ova funkcija je neprekidna, tj. neprekidna na celom svom domenu, a definisana je samo na pozitivnim realnim brojevima.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.



+2801 Profil

icon Re: Muke sa asimtotama28.12.2011. u 18:24 - pre 162 meseci
Citat:
SrdjanR271: Ako je neprekidna nema vertikalnu.


Pardon, ako je realna funkcija definisana na celom R i neprekidna, onda nema vertikalnu asimptotu.

Funkcija je neprekidna i ima vertikalnu asimptotu .
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 
Odgovor na temu

SrdjanR271
Srdjan Radosavljevic
dipl. inženjer informatike

Član broj: 174403
Poruke: 443
*.adsl.eunet.rs.



+88 Profil

icon Re: Muke sa asimtotama28.12.2011. u 18:40 - pre 162 meseci
Slažem se, ali 1/x u nuli ima prekid.

A mathematician is a blind man in a dark room looking for a black cat which isn't there.
 
Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892



+332 Profil

icon Re: Muke sa asimtotama28.12.2011. u 19:20 - pre 162 meseci
Ne, nema, funkcija je neprekidna funkcija, jer je neprekidna na svom domenu, kao sto je Nedeljko lepo rekao.
Tacnije, nije da nema, nego u tacki 0 i ne ispitujemo neprekidnost.
Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.
 
Odgovor na temu

SrdjanR271
Srdjan Radosavljevic
dipl. inženjer informatike

Član broj: 174403
Poruke: 443
*.adsl.eunet.rs.



+88 Profil

icon Re: Muke sa asimtotama28.12.2011. u 20:39 - pre 162 meseci
Šta onda kažemo za tačku x=0, za f-ju 1/x?
A mathematician is a blind man in a dark room looking for a black cat which isn't there.
 
Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892



+332 Profil

icon Re: Muke sa asimtotama28.12.2011. u 20:43 - pre 162 meseci
Citat:
Nedeljko:U tačkama u kojima funkcija nije definisana ona nije ni neprekidna ni prekidna.
Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.
 
Odgovor na temu

SrdjanR271
Srdjan Radosavljevic
dipl. inženjer informatike

Član broj: 174403
Poruke: 443
*.adsl.eunet.rs.



+88 Profil

icon Re: Muke sa asimtotama28.12.2011. u 21:00 - pre 162 meseci
Kako onda definišemo prekide? Ili prekidi ne postoje?

Da li se asimptota računa u prekid?

Pitam jer mi nije jasno, a ne da bih trolovao.

EDIT: Pročitao sam celu temu http://www.elitesecurity.org/t...je-vezi-neprekidnosti-funkcija

http://www.elitesecurity.org/p2717644
Citat:
Jok, prekid je upravo tačka domena u kojoj funkcija nije neprekidna. On je prve vrste ako postoje oba limesa i konačni su (inače je prekid druge vrste), a otklonjiv ako se vrednost u toj tački može promeniti tako da funkcija bude neprekidna. Vidi definiciju.


Može li neki primer takvog prekida? Znači da prekid bude tačka domena, a da nije otklonjiv.


[Ovu poruku je menjao SrdjanR271 dana 28.12.2011. u 22:33 GMT+1]
A mathematician is a blind man in a dark room looking for a black cat which isn't there.
 
Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892



+332 Profil

icon Re: Muke sa asimtotama28.12.2011. u 21:41 - pre 162 meseci
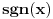
Uzmi na primer funkciju , ona je ocito prekidna funkcija.
Evo, morao sam da uzmem Kadelburga da tacno citiram:
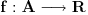
Definicija 5.1.2. Za tacku kazemo da je tacka prekida funkcije ako nije neprekidna u toj tacki.

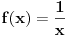
Naglasimo da u skaldu sa ovom definicijom tacka u kojoj neka funkcija nije definisana ne moze biti njena tacka prekida (makar bila i tacka nagomilavanja njene oblasti definisanosti). Tako na primer, tacka nije tacka prekida funkcije , jer, u skladu sa nasom konvencijom datom u odeljku 4.1, za tu funkciju podrazumevamo da joj je domen .
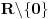
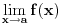
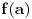
Na osnovu stava 5.1.1, tacke prekida realne funkcije (medju tackama domena koje su ujedno tacke nagomilavanja tog domena) su bilo one tacke kod kojih ne postoji, bilo one kod kojih on nije jednak vrednosti . Uobicajeno je da se tacke prekida klasifikuju na sledeci nacin.
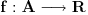
Definicija 5.1.3. Neka je i tacka prekida funkcije . Kaze se da je u tacki :
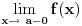
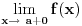
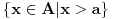
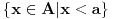
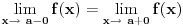
1. prekid prve vrste funkcije ako postoje konacne granicne vrednosti i ; ako je tacka nagomilavanja samo jednog od skupova , , zahteva se samo postojanje jednog (odgovarajuceg) od tih limesa; specijalno, takav prekid je otklonjiv ako je jos , tj. postoji ;
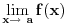
2. prekid druge vrste funkcije ako nije prve vrste.

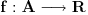
Stav 5.1.1 Neka je funkcija realne promenljive i tacka nagomilavanja skupa . Tada su sledeca tvrdjenja ekvivalentna:
1. funkcija je neprekidna u tacki ;
2.;
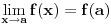
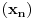
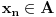
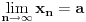
3. za svaki niz , , za koji je , vazi .

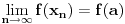
Ne mogu sad da pisem ceo odeljak 4.1.

Citat:
SrdjanR271:
Pitam jer mi nije jasno, a ne da bih trolovao.


Ti si poznat po tome

[Ovu poruku je menjao Sonec dana 28.12.2011. u 23:06 GMT+1]
Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.
 
Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892



+332 Profil

icon Re: Muke sa asimtotama28.12.2011. u 21:49 - pre 162 meseci
Citat:
SrdjanR271:


Može li neki primer takvog prekida? Znači da prekid bude tačka domena, a da nije otklonjiv.


Funkcija ima u tacki prekid prve vrste koji je neotklonjiv. Dok funkcija u toj tacki ima otklonjiv prekid.
Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.
 
Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
212.200.34.*



+391 Profil

icon Re: Muke sa asimtotama28.12.2011. u 22:28 - pre 162 meseci
Ovi decidno kažu da funkcija 1/x u tački x=0 ima prekid druge vrste: http://sh.wikipedia.org/wiki/N...im_vrstama_ta.C4.8Daka_prekida

Ko je sad tu merodavan?

Zabuna je u frazi "funkcija je definisana u tački....".


[Ovu poruku je menjao miki069 dana 28.12.2011. u 23:43 GMT+1]
 
Odgovor na temu

SrdjanR271
Srdjan Radosavljevic
dipl. inženjer informatike

Član broj: 174403
Poruke: 443
*.adsl.eunet.rs.



+88 Profil

icon Re: Muke sa asimtotama28.12.2011. u 22:36 - pre 162 meseci
Hvala na trudu Sonec.

Shvatio sam, sta hocete ti i Nedeljko da kažete.

Ja i dalje neke stvari ne kapiram, ali nemam više pitanja.




A mathematician is a blind man in a dark room looking for a black cat which isn't there.
 
Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892



+332 Profil

icon Re: Muke sa asimtotama28.12.2011. u 22:38 - pre 162 meseci
Citat:
miki069: Ovi decidno kažu da funkcija 1/x u tački x=0 ima prekid druge vrste: http://sh.wikipedia.org/wiki/N...im_vrstama_ta.C4.8Daka_prekida

Ko je sad tu merodavan?

Pa u tacki i jeste prekid druge vrste, nigde nisam (nismo) ni rekli da je prve vrste.

Citat:
SrdjanR271: Hvala na trudu Sonec.

Shvatio sam, sta hocete ti i Nedeljko da kažete.


Nema na cemu
Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.
 
Odgovor na temu

SrdjanR271
Srdjan Radosavljevic
dipl. inženjer informatike

Član broj: 174403
Poruke: 443
*.adsl.eunet.rs.



+88 Profil

icon Re: Muke sa asimtotama28.12.2011. u 22:41 - pre 162 meseci
Citat:
Sonec: 
Pa u tacki i jeste prekid druge vrste, nigde nisam (nismo) ni rekli da je prve vrste.


Onda se može reći da je prekidna na R, a neprekidna na R\{0}?
A mathematician is a blind man in a dark room looking for a black cat which isn't there.
 
Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892



+332 Profil

icon Re: Muke sa asimtotama28.12.2011. u 22:44 - pre 162 meseci
Jezik mi je brzi od pameti. Kao sto sam i pre tvrdio, u tacki ne mozemo da ispitujemo prekidnost.

Ko je upravu, pa rekao bih ipak Kadelburg i Dragoljub Keckic (moj profesor, koji je to isto govorio), Wikipedia nije pouzdana.

Da ne zaboravim, i Dusan Adnadjevic (ipak je i on autor knjige)
Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.
 
Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
212.200.34.*



+391 Profil

icon Re: Muke sa asimtotama28.12.2011. u 22:50 - pre 162 meseci
Nisam ni ja nigde rekao da je prekid prve vrste.
Ako je prekid bilo koje vrste, onda valjda nemamo neprekidnost.
Negacija prekidnosti je neprekidnost.
Negacija neprekidnosti je prekidnost.

Da uprostim pitanje: jel funkcija 1/x prekidna ili neprekidna u x=0?

Ili je sva zabuna nastala od one sintagme "ako je funkcija definisana u tački...", a pre toga se ne obrazlaže dobro šta znači da
je funkcija definisana u tački...?

Imam i ja obe knjige.
Kečkić se na kraju poglavlja tako zaplete, da ne verujem da zna i sam šta je hteo da kaže.


"Onda se može reći da je prekidna na R, a neprekidna na R\{0}?"

Mislim da je ovo jedini ispravan odgovor.
 
Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892



+332 Profil

icon Re: Muke sa asimtotama28.12.2011. u 22:59 - pre 162 meseci
Evo dopuna vezana za poglavlje 4.1:

Pod realnom funkcijom realne promenljive podrazumevacemo svaku funkciju , definisanom na nekom podskupu skupa R realnih brojeva i sa vrednostima u R.
....
Dogovorimo se odmah o sledecem: ako nije drugacije receno, pod domenom realne funkcije realne promenljive date analitickim izrazom podrazumeva se maksimum (u smislu inkluzije) podskupa skupa R koji taj izraz dopusta, tj. .

Za tacku sam vec rekao.
Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.
 
Odgovor na temu

Sonec

Član broj: 284879
Poruke: 892



+332 Profil

icon Re: Muke sa asimtotama28.12.2011. u 23:02 - pre 162 meseci
Citat:
miki069
Kečkić se na kraju poglavlja tako zaplete, da ne verujem da zna i sam šta je hteo da kaže.


Profesor Dragoljub Keckic nije napisao udzbenik iz Analize I.
Leonardo da Vinči

Nema istine u onim naukama u kojima se matematika ne primenjuje.

Milorad Stevanović

Bog postoji zato sto je matematika neprotivurečna.
 
Odgovor na temu

[es] :: Matematika :: Muke sa asimtotama

Strane: 1 2 3

[ Pregleda: 8446 | Odgovora: 44 ] > FB > Twit

Postavi temu Odgovori

Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.