Svi ovi zadaci rade se na "isti" način, bilo da je reč o metodi normalne projekcije i odstojanja, metodi centralne projekcije ili metodi projektovanja na 2 ravni.
Daklem meta-objašnjenja:
1. Oboriš ravan u kojoj je 5-ugaonik, konstruišeš 5-ugaonik, vratiš ga na ravan.
2. Oboriš ravan u kojoj je osnova piramide, nađeš centar osnove, vratiš ga na projekciju, nađeš normalu, oboriš normalu nađeš pravu dužinu SV (S-centar baze, V-vrh piramide), dobiješ V, vratiš na normalu.
3. Ovaj je najjednostavniji po radu te, shodno tome, može da ima najkomplikovanije rešenje.
a) Ako se prave seku, određuju ravan. Oboriš ravan (i prave u njima) izmeriš ugao.
b) Ako su prave paralelne, ugao je 0
c) Ako su prave mimoilazne, konstruišeš ravan koja sadrži jednu od tih pravih, a paralelna je sa drugom. Uradiš normalnu projekciju druge prave na tu ravan, i oboriš ravan. Izmeriš ugao između prve prave i projekcije druge prave i gotovo.
Eh, sad...
Za izračunavanje prave dužine visine možeš koristiti bilo koji pravougli trougao iz piramide npr:
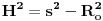
gde je s - bočna ivica, R
o poluprečnik opisane kružnice oko baze (Ovo pod uslovom da su ti sve bočne ivice međusobno jednake). Mislim da ti govoriš o pravilnom jednakoivičnom tetraedru gde je
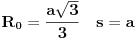
U tom slučaju je
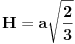
Znači moramo da kostruišemo duž H ako znamo duž a. Uzećemo da je q=a, p=2a/3 (vidi sliku) (Ovo je pomoćna konstrukcija - radi se potpuno odvojeno od zadatka). Posle toga H možemo da koristimo dalje u zadatku.
Za konstruisanje pravilnog petougla ako nam je zadata stranica ima više računa. Ako bismo imali stranicu i poluprečnik opisanog kruga oko 5-ugla, stvar bi bila laka. Nanesemo šestarom dužinu stranice na krug iz poznatog temena i ... dobijemo novo teme. Teme po teme : 5 temena.
Kad bismo imali poluprečnik opisane kružnice... Ali znamo da važi
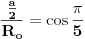
tj
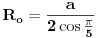
Još samo da znamo taj ugao od 36 stepeni...Postoji dosta načina da ga konstruišemo.
Ako je
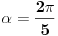
vidimo da je
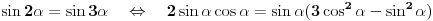
Na kraju dobijemo cos 36.
Ili prvo konstruišem 72, a pola od toga je 36.
No ipak ću ići računski, koristeći zanimljiv šablon.
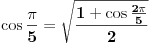
A za 72 stepena...
Označiću sa
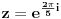
. Sad je z
5=1 tj
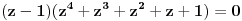
Znamo da
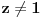
pa
Smena
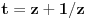de facto znači da je
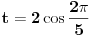
Takođe je
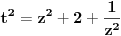
. Jednačina se sad svodi na
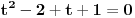
Dakle
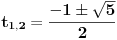
, pa zato
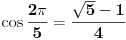
Stoga
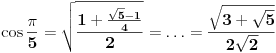
Da bih izračunao
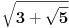
obeležiću sa
a=
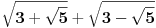
b=
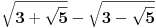
Onda je
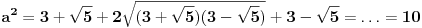
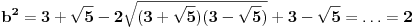
Odatle
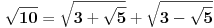
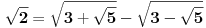
, te najzad
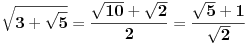
te
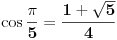Na ovaj način možeš uprostiti mnoge iracionalne izraze
Ovo je ozbiljan zadatak za srednjoškolce, dok na fakultetu spada u poluozbiljne probleme. Naravno mogao si da znaš rešenje i samo da ga ubaciš.
Sad vidimo da je
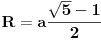
Konstruiši prvo
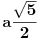
, pa onda i R.
PS Naravno da me mrzi da objašnjavam obaranje prave ili krive, kao i vraćanje iz oborenog u projektovani položaj. To je ipak ono što se prvo nauči.
[Ovu poruku je menjao KPYU dana 25.08.2005. u 22:52 GMT+1]
Nacrtna geometrija
Registrovani: 0 ( 0 )
Re: Nacrtna geometrija
