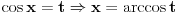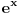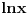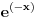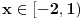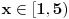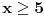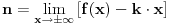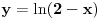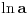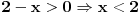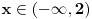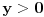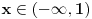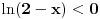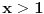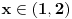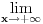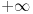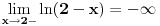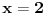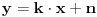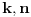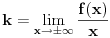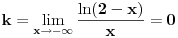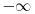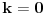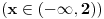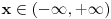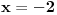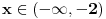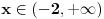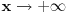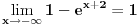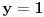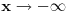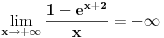4.
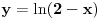
1. Trazimo domen date funkcije, odnosno vrednosti koje

moze da uzima. Logaritamska funkcija
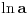
je definisana kada je

, pa shodno tome, nasa posmatrana funkcija je definisana za
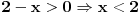
, tj.
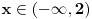
2. Nula funkcije je

. Odredjujemo znak funkcije, kada je pozitivna (
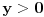
) i kada je negativna (

), pri cemu pazimo da

moze da uzima samo vrednosti iz DOMENA!!! Pa odatle sledi da je

za
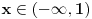
(sto pripada domenu) i
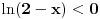
za
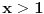
, al s obzirom da

mora pripadati domenu, onda je funkcija negativna za
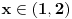
3. Funkcija nije ni parna ni neparna, to je lako da se proveri.
4. Asimptote:
1) horizontalna asimptota

pa ona ne postoji (nismo gledali slucaj
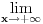
jer

ne moze da tezi ka
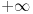
(zbog domena))
2) vertikalna (gledas u granicnim tackama, ovde je to 2, i to limes sa leve strane)
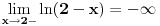
, pa je prava
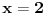
vertikalna asimptota, i

se priblizava njoj sa leve strane u minus beskonacnosti.
3)kosa asimptota je prava oblika
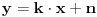
gde se
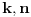
dobijaju iz uslova:
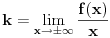
, a za

sam ti vec napisao u mom 1 postu. Aj sad da to primenimo na nas zadatak:
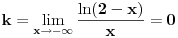
(limes se moze resiti preko lopitala lako, a

tezi samo ka
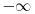
zbog domena (pisao sam to vec za horizontalnu)). S obzirom da je
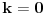
, to je nasa kosa asimptota u stvari horizontalna (

), a ona ne postoji (sto smo vec pokazali), tako da ne postoji ni kosa.
5. Monotonost, nadjes 1 izvod, i dobijas da za
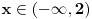
nasa data funkcija opada
6. Konveksnost, drugi izvod (1 izvod na 1 izvodu (koji si vec nasao)), i dobijas da nasa funkcija je konkavna na domenu
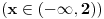
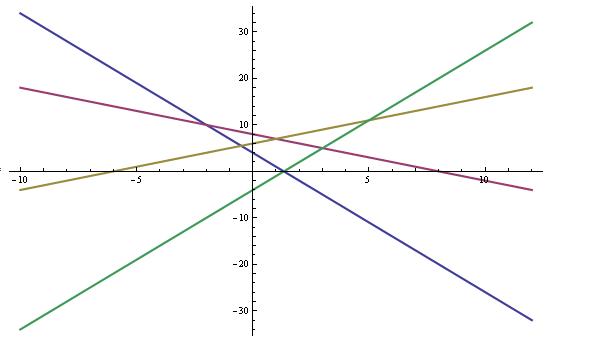
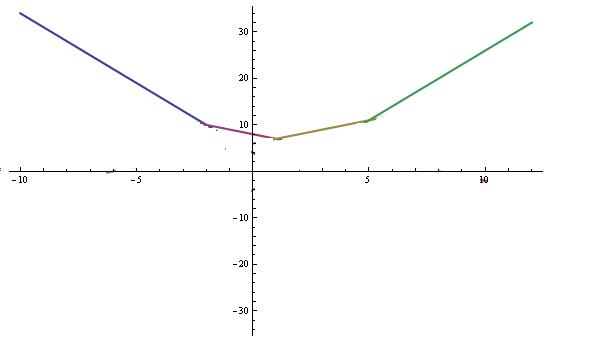
I na kraju ti ostaje da nacrtas grafik
GRAFIK, grafik treba da bude samo realan deo na 2 slici
[Ovu poruku je menjao Sonec dana 15.10.2011. u 01:54 GMT+1]
Leonardo da Vinči
Nema istine u onim naukama u kojima se matematika ne primenjuje.
Milorad Stevanović
Bog postoji zato sto je matematika neprotivurečna.
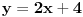 i slicne su mi jasne. Uvek sam izbegavao da pratim nastavu kada su funkcije bile u pitanju, i eto doslo mi glave sada. :(
i slicne su mi jasne. Uvek sam izbegavao da pratim nastavu kada su funkcije bile u pitanju, i eto doslo mi glave sada. :(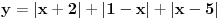
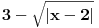
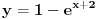
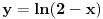
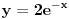
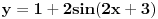
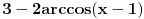 ---> Ovde ne znam sta ovo
---> Ovde ne znam sta ovo 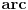 znaci.
znaci.



 Skiciranje nekih lakih funkcija - (treba mi samo objasnjenje)
Skiciranje nekih lakih funkcija - (treba mi samo objasnjenje) Re: Skiciranje nekih lakih funkcija - (treba mi samo objasnjenje)
Re: Skiciranje nekih lakih funkcija - (treba mi samo objasnjenje)