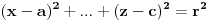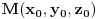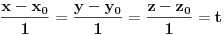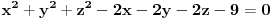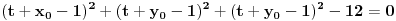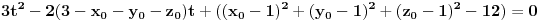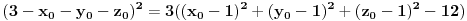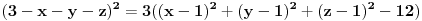Samo cu ti reci da mnogo komplikujes.
Sad resih taj zadatak, dotle sam stigao u onim testovima...
A sada postupak:
napises ovu sferu u kanonskom obliku:
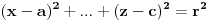
, r je neki broj, poluprecnik
uzmes neku proizvoljnu tacku koja pripada i sferi i cilindru, npr. M(x,y,z).
rastojanje te tacke M od centra sfere C zapravo predstavlja poluprecnik sfere (nacrtaj pa ces videti), i da, sfera pripada tom cilindru, unutar njega je, degenerisani slucajevi nas ne zanimaju...
i sad koristis onu "f-lu" da je vektorski MC (a-x,b-y,c-z) puta vektor ose sfere (koji se ovde poklapa sa osom cilindra, i izgleda (1,1,1)), pa to podeljeno sa intezitetom (normom) od vektora ose (koren iz 3 u ovom slucaju), je jednako normalnom rastojanju od ose, a to upravo predstavlja poluprecnik.....
resis tu jednacinu i dobices kako treba, dobices tacno resenje posto znam koliko je resenje
P.S ja ne videh onaj kod za alokaciju liste sto te pitah

Leonardo da Vinči
Nema istine u onim naukama u kojima se matematika ne primenjuje.
Milorad Stevanović
Bog postoji zato sto je matematika neprotivurečna.
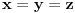 koji dodiruje sferu
koji dodiruje sferu 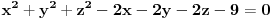 .
.



 Zadatak iz analitičke geometrije
Zadatak iz analitičke geometrije