Pošto je kongruencija

refleksivna relacija na G, vrijedi:
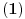
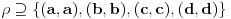
.
Pošto je kongruencija

i simetrična i tranzitivna relacija na G, vrijedi:
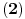
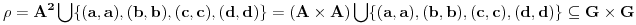
.
Imamo dvije kongruencije:
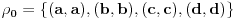
i
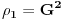
.
Da bi našli sve kongruencije moramo naći sve podgrupoide grupoida (
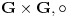
) koji sadrže
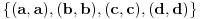
, gdje je operacija

definisana na sledeći način:
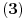
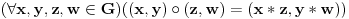
.
Iz
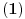
,
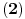
i
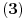
slijedi da je
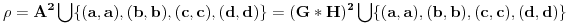
, gdje je H podgrupoid od G takav da vrijedi:
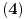
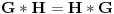
.
Podgrupoidi od G su:
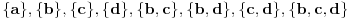
.
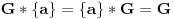
, dakle,
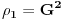
.
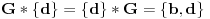
, dakle,

.
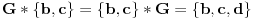
i
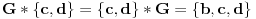
i
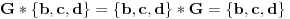
, dakle,
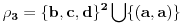
.
Za podgrupoide
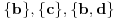
ne vrijedi
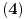
. Odredili smo četiri kongruencije grupoida G.
Da postoje pogrupoidi od G takvi da su njihovi odgovarajući proizvodi sa G međusobno disjunktni i vrijedi (4) za svaki od njih, kod određivanja kongruencija za A bi uzeli njihove disjunktne unije.
[Ovu poruku je menjao Sini82 dana 07.05.2011. u 12:41 GMT+1]