[es] - čudnovat broj e

edisnp

Član broj: 269233
Poruke: 478
*.adsl.eunet.rs.

+27 Profil

^{22.04.2011. u 14:23 - pre 170 meseci}

Culi ste svi za Dijsktrin algoritam za nalazenje najkraceg puta koji se
razvija i programiranje i matematickim putem preko nekakvih grafova.

حياتي هو العلم بلدي (الرياضيات)

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.proxyboost.nl.

+443 Profil

Re: čudnovat broj e

^{22.04.2011. u 14:32 - pre 170 meseci}

Citat:

^Nedeljko

ali ne tako kako si zamislio.

Šta sam zamislio?

Citat:

^SrdjanR271

pow je "dobar" ali ne zna limese

Pa sad, kako da ti kažem, taj c-program što sam napisao je samo računanje stepena a ne limesa. U stvari u celoj ovoj temi do sada nisam pomenuo limes.

Osim toga, forumule koje sam izveo treba da pokažu zašto se binom

ne može svesti na 1 čak i za velike vrednosti n jer je dobijen izraz koji samo u specijalnom slučaju x=0 postiže vrednost 1.

Umesto da se diskusija širi u nepotrebnom smeru mogao bi neko da ospori izvodjenje ako može ili da pokaže na drugi način.

_{[Ovu poruku je menjao kandorus dana 22.04.2011. u 16:36 GMT+1]}

Odgovor na temu

SrdjanR271
Srdjan Radosavljevic
dipl. inženjer informatike

Član broj: 174403
Poruke: 443
*.adsl.eunet.rs.

+88 Profil

Re: čudnovat broj e

^{22.04.2011. u 15:07 - pre 170 meseci}

Citat:

edisnp: Culi ste svi za Dijsktrin algoritam za nalazenje najkraceg puta koji se
razvija i programiranje i matematickim putem preko nekakvih grafova.

Jesmo. I šta sa njim?

A mathematician is a blind man in a dark room looking for a black cat which isn't there.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: čudnovat broj e

^{22.04.2011. u 16:54 - pre 170 meseci}

Ni pow nije "dobar", jer pravi računsku grešku.

Citat:

kandorus: Šta sam zamislio?

Pa, pomenuo si taj program i dokazivanje teorema pomoću računara. U tom dokazivanju se ne koriste "grešne" stvari kao što je FPU, osim kada je ta greška pod kontrolom.

Citat:

kandorus: Osim toga, forumule koje sam izveo treba da pokažu zašto se binom

ne može svesti na 1 čak i za velike vrednosti n jer je dobijen izraz koji samo u specijalnom slučaju x=0 postiže vrednost 1.

Binom ima vrednost 1 i za

. Za konačne vrednosti

ne. Naravno, u prvom slučaju je beskonačan stepen jedinice nedefinisan.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: čudnovat broj e

^{22.04.2011. u 19:08 - pre 170 meseci}

Nedeljko:

Citat:

Savetujem ti da naučiš realne brojeve.

Hvala na savetu! Potrudiću se. U međuvremenu ću se poslužiti tvojim iskustvom iznetim ovde.
Nadam se da nemaš ništa protiv.U jednoj poruci napisao si ovo:

za svako

(Ova formula je baš zgodna za dokazivanje koliko je

i koliko je

)
Neka je z = 0. Budimo malo i formalisti pa to i napišimo:

Vrednost u zagradi je, prema tome, jednaka 1 i ta vrednost se beskonačno puta množi sama sa sobom
i dobijamo da je rezultat jednak 1 zato što je

Zar može biti jednostavniji dokaz?
Međutim, ako ako umesto z = 0 stavimo da je z = 1 onda dobijamo

, a broj e nije
jednak 1 nego 2,71828… Odakle sad ta razlika od 1,71828… kad je po tvom iskustvu

pa se ni u zagradi ni nad zagradom ništa nije promenilo ?
Stvar je potpuno jasna – 1/∞ se ne može poistovećivati sa nulom već je to beskonačno mala vrednost za koju
je izraz u zagradi veći od 1 i kad se taj izraz beskonačno puta pomnoži sa sobom dobija se broj e.
To takođe znači da je 1/∞ ≠ 2/∞ ≠ 3/∞ ≠ 5/∞ i t. d. Ako ne veruješ uveri se jer se po gornjoj
formuli dobijaju limesi 1, e, e², e³, e⁵
Dakle, ako je jedinica sama onda je 1^∞ = 1, a ako nije sama onda rezultat zavisi od «društva» i
samo zbog tog društva kaže se da je 1^∞ nedefinisano jer rezultat od njega zavisi tako kako je pokazano
i kako još može biti.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: čudnovat broj e

^{22.04.2011. u 20:11 - pre 170 meseci}

Citat:

atelago: Hvala na savetu! Potrudiću se.

Pa, potrudi se. Ovako ne možemo da raspravljamo, jer ne poseduješ elementarna potrebna znanja. Nabavi bilo koji užbenik matematičke analize 1 za matematički fakultet. Tamo ćeš naći aksiome polja realnih brojeva, definiciju limesa, metode računanja itd.

Za početak, u polju realnih brojeva ne postoje beskonačno male veličine, a u proširenom skupu realnih brojeva je

jedna jedina konstanta, tj. nema razli;itih beskona;nosti.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.proxyboost.nl.

+443 Profil

Re: čudnovat broj e

^{22.04.2011. u 23:17 - pre 170 meseci}

Citat:

atelago
To takođe znači da je 1/∞ ≠ 2/∞ ≠ 3/∞ ≠ 5/∞ i t. d. Ako ne veruješ uveri se jer se po gornjoj
formuli dobijaju limesi 1, e, e², e³, e⁵

2/∞ = 2/(2*∞) = 1/∞ = 0

Budući da je limes proizvoda jednak proizvodu limesa dobija se:

Iz poslednjeg izraza može se uočiti da su članovi (1-1/n), (1-2/n), ..., (1-(n-2)/n), (1-(n-1)/n) uvek prisutni bez obzira kolika je vrednost x. Vrednost stepena broja e odredjuje član x^k/k!. Zato što, za male vrednosti k proizvod (1-1/n)(1-2/n), ..., (1-(k-1)/n) teži 1 a kad k->∞ tada proizvod (1-1/n)(1-2/n), ..., (1-(k-1)/n) teži 0 jer i n->∞.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: čudnovat broj e

^{23.04.2011. u 00:20 - pre 170 meseci}

Citat:

kandorus: Budući da je limes proizvoda jednak proizvodu limesa

Samo ako imaš fiksan konačan broj činilaca, tj. za svako

važi: Ako su

konvergentni nizovi, onda je niz

konvergentan i tačna je jednakost

.

No, u načem slučaju je broj činilaca promenljiv i teži beskonačnosti.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.proxyboost.nl.

+443 Profil

Re: čudnovat broj e

^{23.04.2011. u 07:47 - pre 170 meseci}

Samo što taj beskonačni proizvod nije razlagan!
Obrati pažnju, razlaganje je izvršeno na dva člana!

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: čudnovat broj e

^{23.04.2011. u 09:07 - pre 170 meseci}

Jao, tek sad vidim šta si napisao. U poslednjem redu ti se pojavljuje n van limesa. To tek nema smisla.

Treba ti nešto ovako:

.

To važi pod uslovom da je

za svako

, što je svakako ispunjeno.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.proxyboost.nl.

+443 Profil

Re: čudnovat broj e

^{23.04.2011. u 10:12 - pre 170 meseci}

Gde se "pojavljuje n van limesa"?

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: čudnovat broj e

^{23.04.2011. u 10:54 - pre 170 meseci}

Opet nisam dobro video. Ne pojavljuje se van limesa, ali ne vidim da poslednji red ima smisla. Koliko imaš sabiraka u poslednjem redu? Obzirom da si napisao

kao poslednji sabirak, reklo bi se da sabiraka ima konačno mnogo, ali nije jasno koliko.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.proxyboost.nl.

+443 Profil

Re: čudnovat broj e

^{23.04.2011. u 11:35 - pre 170 meseci}

Pa dodaću tri tačke i ako uvedem opšti k-ti član uz prelom reda onda je pogodnije za pregled:

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: čudnovat broj e

^{23.04.2011. u 11:54 - pre 170 meseci}

Bezveze je što je

pod limesom, a

nije, pa zbunjuje, mada je to naravno isto.

Dakle, pikiraš na

,

a imao si

.

Za tu razmenu mesta limesa i sume ti treba onaj uslov koji sam napisao i koji je svakako ispunjen.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: čudnovat broj e

^{23.04.2011. u 12:20 - pre 170 meseci}

Nedeljko:

Citat:

Ovako ne možemo da raspravljamo, jer ne poseduješ elementarna potrebna znanja.

Znanja, pogotovu elementarna su svakako potrebna, ali su beskorisna ukoliko ne posedujemo
elementarnu moć rasuđivanja. Na primer nije bitno da li u polju realnih brojeva postoje
infinitezimale ili ne, ako nam one u konkretnom slučaju služe da rešimo neki problem. Kad
integrališ neku površinu onda je elementarna površina dF = f(x)dx. Koliki je diferencijal dx?
Koliko takvih diferencijala može stati na 1 cm dužine apscise? Stvarno ne razumem šta si
hteo da kažeš.
Drugo: Mislim da nigde nisam govorio o različitim beskonačnostima.
Treće: Ne govoriš o problemu odnosno o temi. Budi ljubazan pa mi kaži gde si našao greške
u mojoj prethodnoj poruci i saopšti ih. Bilo bi fer.To treba činiti u dobroj nameri.

Kandorus:

Citat:

2/∞ = 2/(2*∞) = 1/∞ = 0

Prihvatam šalu i dodajem: nije 2/∞ jednako 1/∞ nego 4/∞. Evo pogledaj 2/∞ = 2/(0,5*∞) = 4/∞.
Ovo je bila šala, ali ovo nije šala nego greška:

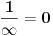
jer nije u saglasnosti s ovim:

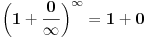
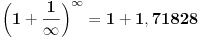
Sta je uzrokovalo drukčiji rezultat u drugoj jednačini?
Ovo su dva realna broja koja postoje nezavisno od toga da li su limesi nekih nizova ili nisu.
Pogrešno je reći «broj e je limes». Broj e je realan broj kao i ostali realni brojevi i on može
biti limes niza kao što i ostali realni brojevi mogu biti limesi nekih nizova. Broj e ne teži nikuda
on je konstanta koja se ne dobija kada «n teži ka beskonačno» nego kada n jeste beskonačno.
Težnja se odnosi na članove niza koji mu se približavaju a ne na njega, a on, konkretno,
čak i nije član toga niza.

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: čudnovat broj e

^{23.04.2011. u 15:56 - pre 170 meseci}

Atelago, mogu li samo priupitati šta je O u tvom imenu? Da li, kad se čita unatrag, stoji kao prvo slovo od osveta galeta, ili si neku drugu reč imao u vidu?

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

SrdjanR271
Srdjan Radosavljevic
dipl. inženjer informatike

Član broj: 174403
Poruke: 443
*.dynamic.isp.telekom.rs.

+88 Profil

Re: čudnovat broj e

^{23.04.2011. u 16:45 - pre 170 meseci}

Citat:

Bojan Basic: Atelago, mogu li samo priupitati šta je O u tvom imenu? Da li, kad se čita unatrag, stoji kao prvo slovo od osveta galeta, ili si neku drugu reč imao u vidu?

Bravo. I da nije galet, svaka čast za zapažanje. Ne bi mi nikad palo na pamet.

A mathematician is a blind man in a dark room looking for a black cat which isn't there.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: čudnovat broj e

^{23.04.2011. u 17:21 - pre 170 meseci}

I ja sam pomislio da je galet, ali me je pokolebao kada je na trenutak rekao da je voljan da uči! No, poslednjom porukom se razotkrio, pa mu nisam odgovarao.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

kandorus

Član broj: 266404
Poruke: 429
*.proxyboost.nl.

+443 Profil

Re: čudnovat broj e

^{23.04.2011. u 19:45 - pre 170 meseci}

Citat:

atelago
Ovo je bila šala, ali ovo nije šala nego greška:
1/∞ = 0
jer nije u saglasnosti s ovim:
(1 + 0/∞)^∞ = 1 + 0
(1 + 1/∞)^∞ = 1 + 1.71828
Sta je uzrokovalo drukčiji rezultat u drugoj jednačini?

Kad se uključi simbol ∞ onda taj izraz ne znači da se množenje i deljenje vrši kao u osnovnoj školi (n binoma se pomnoži) već se moraju uzeti u obzir pravila koja važe za granične vrednosti. Transformacijom izraza pre prelaska na granične procese vidi se zašto se dobijaju različiti rezultati. Upravo zato sam izdvojio opšti član:

Ono što posebno odreduje vrednost stepena (e^x) je član x^k/k!.

Iz datog izraza se vidi da je promenljiva x (kojom se stepenuje e) izdvojena iz limesa proizvoda. Unutar limesa proizvoda se javljaju konstante nezavisne od x. Konstante su iz skupa {1, 2, ..., k-1} i iste su za svako x. Zato je vrednost limesa proizvioda ista za odgovarajući član sabirka i nezavisna od vrednosti promenljive x.

Nakon tih transformacija može da se predje na granični proces te se za opšti član sume dobija vrednost

gde je 0 < a_k < 1. Još jednom, a_k ne zavisi od x.

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: čudnovat broj e

^{16.07.2011. u 20:40 - pre 167 meseci}

Citat:

Bojan Basic:
Atelago, mogu li samo priupitati šta je O u tvom imenu?

Možeš! Upravo si to i učinio. U mom imenu nema slova O.

Citat:

Da li, kad se čita unatrag, stoji kao prvo slovo od osveta galeta, ili si neku drugu reč imao u vidu?

Zašto bih ja osvećivao galeta? Da li sam mojim porukama nekom naneo zlo koje liči na osvetu?
Nekada sam živeo u Babinu Potoku pored Plitvica. Otuda i potiče "ate lago".
Pošto sam poistovećen sa galetom neko vreme nisam imao pristup ovde, pa nisam mogao da
odgovorim, slučajno sam otkrio da mogu da se ulogujem i to sada koristim ukoliko me sličnost sa
galetom ne diskvalifikuje.

Odgovor na temu