[es] - Teorija brojeva

sannyy
student

Član broj: 277235
Poruke: 49
*.customer.blic.net.

Profil

^{01.02.2011. u 13:12 - pre 173 meseci}

Eulerova funkcija je multiplikativna, tj. ako su m i n relativno prosti, onda vrijedi fi(m*n)=fi(m)*fi(n).
Moze li ni neko pomoci oko dokaza ove teoreme?

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
89.216.32.*

+2801 Profil

Re: Teorija brojeva_Teoreme

^{01.02.2011. u 14:21 - pre 173 meseci}

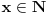
neka je

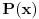
skup svih prirodnih brojeva ne većih od

, koji su uzajamno prosti sa

i neka je

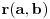
ostatak pri delenju prirodnog broja

prirodnim brojem

. Sa

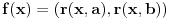
definisana je jedna bijekcija skupa

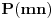
u skup

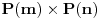
. Pokušaj to da dokažeš.

Ako su

uzajamno prosti, onda je

uzajamno prosto sa

akko je uzajamno prosto kako sa

, tako i sa

. Odatle sledi dobra definisanost funkcije

.

Odatle i iz kineske teoreme o ostacima sledi da je ta funkcija surjektivna.

Ako je

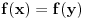
, onda je

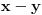
deljivo kako sa

, tako i sa

. Stoga je deljivo i sa

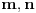
, što je na datom domkenu moguće samo za

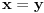
. Odatle sledi injektivnost.

To ti je skica, pa je upotpuni.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

sannyy
student

Član broj: 277235
Poruke: 49
*.customer.blic.net.

Profil

Re: Teorija brojeva_Teoreme

^{01.02.2011. u 21:38 - pre 173 meseci}

Hvala... pokusacu sad da se malo zabavim ovim...
A evo dokaza koji meni i nije bas legao... ide ovako...
Neka je nzd(m,n)=1 i neka a i b prolaze reduciranim sistemom ostataka modulo m, odnosno modulo n.
Eh cilj je pokazati da an+bm prolazi reduciranim sistemom ostataka modulo mn... i ako se to pokaze dobije se da je fi(mn)=fi(m)*fi(n) ( a meni nije jasno kako se to dobije)
Dalje...
Kako je nzd(a,m)=1 i ndz(b,m)=1, to je broj an+bm relativno prost s m i s n (nejasno)
Svaka dva broja takvog oblika su nekongruentni modulo mn.
Iz an+bm==a'n+b'm(mod mn) slijedi (a-a')n==(b'-b)m (mod mn), odavde m|a-a' i n|b'-b, pa je a=a' i b=b'.
Treba pokazati jos da ako je nzd(c,mn)=1 da je c==an+bm (mod mn) za neke a i b.
Kako je ndz(m,n)=1 to postoje cijeli brojevi x i y takvi da je mx+ny=1.
Ocito je nzd(cy,m)=1 i nzd(cx,n)=1, pa brojevi a i b definirani s cy==a (modm) i cx==b (modn) imaju trazena svojstva.

Odgovor na temu

sannyy
student

Član broj: 277235
Poruke: 49
*.customer.blic.net.

Profil

Re: Teorija brojeva_Teoreme

^{01.02.2011. u 22:59 - pre 173 meseci}

Evo jos jedne teoremice...
Neka su a i m prirodni brojevi, te b cijeli broj. Kongruencija ax==b (mod m) ima rjesenje akko d= nzd(a,m) dijeli b.
Ako je ovaj uvijet zadovoljen, onda gornja kongruencija ima tacno d rjesenja modulo m.

Dokaz:

Ako kongruencija ax==b (mod m) ima rjesenje onda postoji y iz skupa cijelih broojeva tako da je ax-my=b.
Tada imamo da nzd(a,m) dijeli b. Pretpostavimo da d=nzd(a,m) dijeli b. Stavimo da je a'=a/d, b'=b/d i m'=m/d. ( zasto uzimamo ovo a' i b'?)
Sada trebamo rijesiti kongruenciju a'x==b' (modm'). Nzd(a',m')=1, pa x prolazi potpunim sistemom, tj. svaki ostatak mod m' (pa tako i b')se dobija tacno za jedan x iz potpunog sistema ostataka mod m'.
Ako je x' rjesenje kongruencije a'x'==b' (mod m'), onda su sva rjesenja od ax==b (mod m) u cijelim brojevima dana s x=x'+nm', n je prirodan broj,
a sva neekvivalentna rjesenja dana su s x=x'+nm', n=0,1,2,3, ... ,d-1.
Dakle, ako d dijeli b, onda kongruencija ax==b (mod m) ima tacno d rjesenja mod m

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
89.216.32.*

+2801 Profil

Re: Teorija brojeva_Teoreme

^{02.02.2011. u 09:23 - pre 173 meseci}

za neke

. Pritom je

uzajamno prosto sa

, a

uzajamno prosto sa

. Neka je

uzajamno prosto sa

. To tačno znači da je

uzajamno prosto sa

. No, tada je

, kao i

. Ako je

, onda je

. Može se na primer uzeti da je

ostatak pri delenju

, a

ostatak pri delenju

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

sannyy
student

Član broj: 277235
Poruke: 49
*.customer.blic.net.

Profil

Re: Teorija brojeva_Teoreme

^{05.02.2011. u 11:22 - pre 173 meseci}

Osnovna teorema aritmetike
Faktorizacija svakog prirodnog broja n>1 na proste faktore je jedinstvena, do na poredat prostih faktora.

Dokaz:
Pretpostavimo suprotno, tj. da postoje dvije razlicite faktorizacije broja n.
Dijeljeci te dvije faktorizacije s prostim brojevima koji su zajednicki objema reprezentacijama, dobicemo jednakost oblika:
p1*p2*...*pk=q1*q2*...*ql
gdje su pi i qi prosti brojevi, ne nuzno razliciti, ali takav da se nijedan prost broj s lijeve strane ne pojavljuje na desnoj.
Medjutim, jer iz p1|q1*q2*...*ql (nije mi jasno otkud ovo), slijedi da p1 dijeli barem jedan qi, a to je kontradikacija.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.mts.telekom.rs.

+2801 Profil

Re: Teorija brojeva_Teoreme

^{05.02.2011. u 18:17 - pre 173 meseci}

Neka je

.

Iz

sledi da

, a odatle i iz

. No, obzirom da je

prost broj, odatle sledi da

za neko

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

sannyy
student

Član broj: 277235
Poruke: 49
*.customer.blic.net.

Profil

Re: Teorija brojeva_Teoreme

^{05.02.2011. u 18:26 - pre 173 meseci}

Razumjela. :)
Hvala!

Odgovor na temu

nikmil

Član broj: 45895
Poruke: 55
217.26.76.*

Profil

Re: Teorija brojeva_Teoreme

^{06.02.2011. u 15:20 - pre 173 meseci}

Evo još jednog dokaza multiplikativnosti Ojlerove funkcije.
Broj automorfizama ciklične grupe

jednak je upravo

.
Lako se dokazuje da za uzajamno proste

važi

, pa je

Odgovor na temu

sannyy
student

Član broj: 277235
Poruke: 49
*.customer.blic.net.

Profil

Re: Teorija brojeva_Teoreme

^{10.02.2011. u 16:30 - pre 173 meseci}

Moze li mi neko pomoci oko dokaza Wilson-ove teoreme...
Ako je p prost broj, onda je (p-1)!==-1 (mod p). ?

Odgovor na temu

sannyy
student

Član broj: 277235
Poruke: 49
*.customer.blic.net.

Profil

Re: Teorija brojeva_Teoreme

^{14.02.2011. u 17:09 - pre 172 meseci}

Dokaz Wilson-ove teoreme:
Za p = 2 i p = 3 kongruencija je ocito zadovoljena.
Pretpostaviti da je p>=5. Grupirajmo clanove skupa {2,3,..., p-2} u
parove (i,j) sa svojstvom i * j ==1 (mod p).
Ocito je i razlicito od j jer bi inace broj (i - 1)(i + 1) bio djeljiv sa p,
a to je nemoguce zbog 0 < i ¡ 1 <i + 1 < p.
Tako dobivamo p-3/2 parova i ako pomnozimo odgovarajucih p-3/2
kongruencija, dobicemo
2 * 3 *...* (p - 2) == 1 (mod p);
pa je
(p -1)!== 1(mod p).

Odgovor na temu