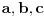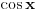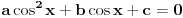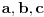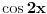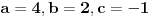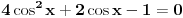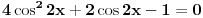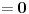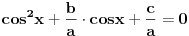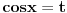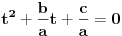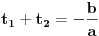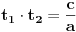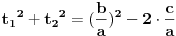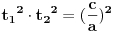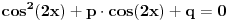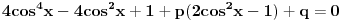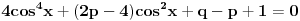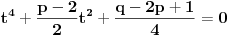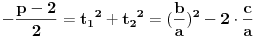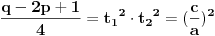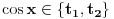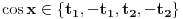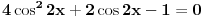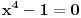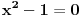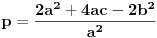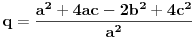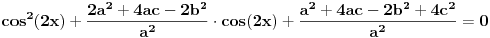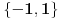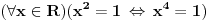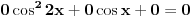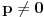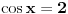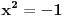E, sad, ako su rešenja jednačine
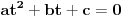 po
po  recimo
recimo 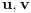 , onda je polazna jednačina ekvivalentna sa
, onda je polazna jednačina ekvivalentna sa 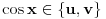 , pa je
, pa je 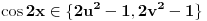 . No, poslednja relacija je zapravo ekvivalentna sa
. No, poslednja relacija je zapravo ekvivalentna sa 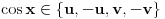 , što je ekvivalentno polaznoj jednačini akko je
, što je ekvivalentno polaznoj jednačini akko je 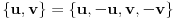 , odnosno akko je
, odnosno akko je 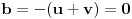 . Dakle, ako je
. Dakle, ako je 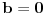 , onda je polazna jednačina ekvivalentna jednačini
, onda je polazna jednačina ekvivalentna jednačini 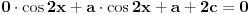 , a inače nema rešenja, tako da drugi deo zadatka nema smisla.
, a inače nema rešenja, tako da drugi deo zadatka nema smisla.Molio bih druge da iznesu neki komentar o ovome.
[Ovu poruku je menjao Nedeljko dana 17.01.2011. u 15:37 GMT+1]




 Čudan zadatak sa prve međunarodne matematičke olimpijade (Rumunija 1959)
Čudan zadatak sa prve međunarodne matematičke olimpijade (Rumunija 1959)