Ja kod ovakvih zadataka imam sledeći pristup:
1)Naći determinantu sistema
Ovde je to:
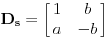
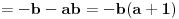
Ako je
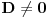
, tj.
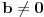
i
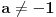
tada je sistem određen i ima jedinstveno rešenje.
Razmotrimo slučajeve kada je
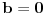
i(li)
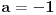
.
1)
Neka je b=0, a
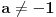
.
Sistem postaje:
x=0
ax=0
Sistem ima tačno određenu vrednost x=0, ali y može biti proizvoljno, pa je tada sistem neodređen.
2)
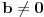
i
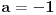
Sistem postaje:
x+by=0
x-by=b
Odatle je sabiranjem
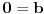
, što je protivno polaznom uslovu da je
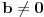
, pa je u tom slučaju sistem kontradiktoran.
Valjda je ovo što sam napisao dobro

.
I imam i ja jedno malo pitanje, šta znači da je sistem više puta neodređen? Da li to znači da recimo ako je kao ovde sa dve nepoznate da postoji beskonačno mnogo x i y koji zadovoljavaju jednačinu, a 1 put je neodređen ako jedna promenljiva može imati beskonačno mnogo vrednosti, a druga je strogo određena? Nisam sreo taj termin " n puta neodređena", pa zato pitam.
Ako je tako kako sam napisao sasvim je logično da ova jednačina bude 1 put neodređena, a ne i dva puta.