Tako mi i treba kad u
nedoba kucakam postove.
Pokušaću da složim priču koja ima kraj & početak.
Pretpostavimo da imamo polinomnu j-nu
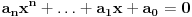
, gde su svi a
i celi brojevi. Mi želimo da nađemo racionalne nule oblika
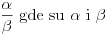
takođe celi brojevi, ukoliko takve nule postoje.
Znamo da
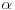
mora da deli a
0, i da
mora da deli a
n
U ovom slučaju
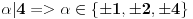
, jer su to svi celi delioci broja 4 (najmlađeg koeficijenta u našem polinomu).
Eh sad,
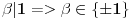
, jer su to svi delioci najstarijeg koeficijenta u našem polinomu.
Pošto
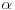
može biti i negativan broj, možemo da se zadržimo da kažemo da je
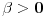
dakle
.
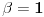
Daću i drugi primer:
.
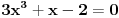
Vidimo da
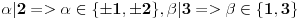
. OBRATI PAŽNJU rekao sam
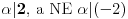
, jer x|y <=> x|(-y) <=> (-x)|y
Dakle racionalne nule mogu biti
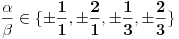
, tj
nabadamo samo za vrednosti iz skupa {
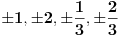
}. Ovde, sa žaljenjem, konstatujemo da
nema racionalnih nula :(
Napominjem ova jednačina nema racionalnih, ali ima iracionalnih nula. Njih, naravno ne možemo da nađemo ovakvom metodom, niti da ih
nabadamo ikakvom metodom.
Eh, još samo da napomenem kakve veze ima traženje nula sa razlaganjem polinoma. Kao što reče moj imenjak Peddja, Bezuov stav: Ako je x
0 nula polinoma (tj rešenje jednačine p(x)=0), tada je polinom p(x) deljiv polinomom (x-x
0)
Jos jedno rastavljanje na cinioce - kako?
Registrovani: 0 ( 0 )
