[es] - Popmoc oko zadatka iz kinematike..

lazamil

Član broj: 175094
Poruke: 5
*.dynamic.isp.telekom.rs.

Profil

^{23.11.2010. u 20:01 - pre 175 meseci}

Pokusavao sam da provalim kako se resava, ali mi ne ide. Radi se nekako preko trenutnog pola i odredjivanja ubrzanja i brzine na osnovu vec poznatih ali ne znam kako se to radi. Svaka pomoc i predlog su dobro dosli, pored ovog imam i par slucajeva sa kvadratom, rombom i nekim drugim oblicima plocice. Hvala na pomoci...

Odgovor na temu

NicholasMetropolis
NicholasMetropolis
Beograd

Član broj: 220441
Poruke: 283
*.adsl.alicedsl.de.

+17 Profil

Re: Popmoc oko zadatka iz kinematike..

^{27.11.2010. u 11:45 - pre 175 meseci}

Izvini što tek sada odgovaram, ali skroz sam zaboravio na ovaj zadatak pored drugih stvari na forumu.

Na osnovu toga kako si postavio zadatak rekao bih da si mašinac ili građevinac. Vi verovatno imate neke konstruktivne fore na koje rešavate ove zadatke. Pošto ih ja ne znam, uradiću onako kako znam što možda i nije najbolje za tebe, jer je na ovom primeru očigledno šta se dešava i bez primene bilo kakvih konstrukcija.

Dakle, imamo pločicu koja je jednakostranični trougao. Dole sam nacrtao sliku.

Ubrzanje temena B mora biti kao na slici zato što je pločica čvrsto telo a jedino ubrzanje kao na slici osigurava da se rastojanje između temena ne menja. Šta ovo znači? Ovo znači da pločica ubrzano rotira oko svog težišta (pošto se kod jednakostrančnog trougla težište i centar opisanog kruga poklapaju). Dakle odmah zaključujemo da je ubrzanje težišta nula. Sa slike je onda lako odrediti intenzitete tangencijalnog i centripetalnog ubrzanja.

#define TRUE FALSE /*Happy debugging suckers*/

Odgovor na temu

Fermion
ucenik

Član broj: 273771
Poruke: 237
*.mbb.telenor.rs.

+13 Profil

Re: Popmoc oko zadatka iz kinematike..

^{27.11.2010. u 13:00 - pre 175 meseci}

Dakle trougaona ploča je celina i rastojasnje između temena trougla u svakom trenutku mora biti isto.

Temena A i D imaju ubrzanja jednakih intenziteta. U odnosu na tačku B, tačke A i D miruju. To znači da je ubrzanje tačke B u odnosu na A, D nula. Ako vektore ubrzanja temena A i D transliramo u tačku B tako da im se početak poklopi sa tom tačkom onda će rezultujuće ubrzanje biti rezultat slaganja ubrzanja od pojedinačnih temena, a ubrzanje temena B biće usmereno suprotno od vektora

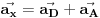
, gde je ugao između vektora

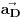
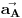
ima vrednost

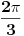
. Odatle se nalazi

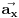
, dok je

.

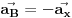
Prema tome intenzitet ubrzanja temena B je takođe

. Njegov pravac odgovara stranici

, a smer je prema temenu A kao što je pokazano na slici u prethodnoj poruci.

Oko trougla opišimo krug. Ako vektor ubrzanja razložimo na dve komponente, tangencijalnu i normalnu, onda će tangencijalno i normalno ubrzanje svake od tačaka A, B, D biti istog intenziteta. Prema tome možemo zaključiti da trougao rotira tako da mu temena u svakom trenutku budu na tom krugu. Tačka kroz koju prolazi osa rotacije ne vrši translatorno kretanje, i intenzitet ubrzanja te tačke iznosi 0. Centar rotacije odgovara centru opisanog kruga, tj. samom težištu trougla, pa je ubrzanje težišta takođe 0.

Dakle:

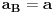
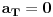_{[Ovu poruku je menjao Fermion dana 27.11.2010. u 14:45 GMT+1]}

_{[Ovu poruku je menjao Fermion dana 27.11.2010. u 14:54 GMT+1]}

Odgovor na temu