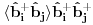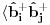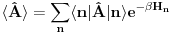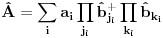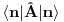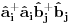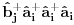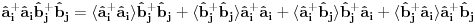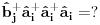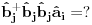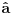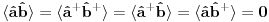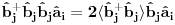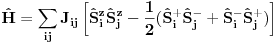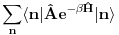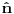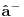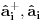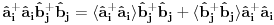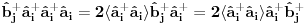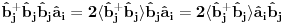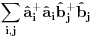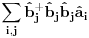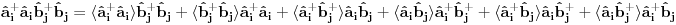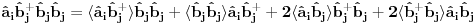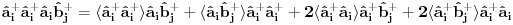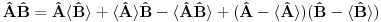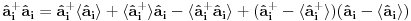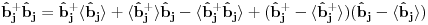Nisam siguran da je ovo tačno, zato što ako su
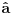
i
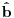
anihilacioni operatori za različite vrste čestica, onda imaš da je
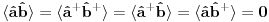
Na osnovu ovoga mislim da bi trebali da imamo:

i
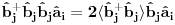
E da, i zašto se ovo zove self-consistent spin wave theory:
Kada npr imaš Hajzenbergov hamiltonijan
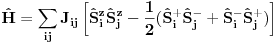
, nalaženje očekivane vrednosti bilo kog operatora podrazumeva izračunavanje
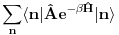
(1)
što je u opštem slučaju nemoguće uraditi analitički zbog prisustva eksponencijalne funkcije. Prva stvar je da mapiraš operatora spina na operatore druge kvantizacije. To možeš da uradiš pomoću Holšten-Primakov, Dajson Maleev ili nekih drugih transformacija. Pošto tada u razvoju eksponencijalne funkcije imaš proizvode operatora
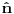
,

i
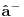
, problem pojednostavljuješ tako što proizvod većeg broja operatora svedeš na sumu proizvoda sa manjim brojem operatora (ono dekuplovanje koje si ti radio) tako što određeni broj operatora zameniš njihovim srednjim vrednostima. Naravno, ovde se vrtiš u krug, pošto, da bi izračunao srednju vrednost moraš biti u stanju da izračunaš (1), a ovu aproksimaciju smo uveli da bismo upravo izračunali (1).
Kako se izlazi iz ovog začaranog kruga? Tako što pretpostavimo da je problem samokonzistentan. Tj. pretpostavimo početne očekivane vrednosti, ubacimo ih u (1) i izračunamo nove očekivane vrednosti pa onda ceo proces ponavljamo. Ako je problem samokonzistentan, očekujemo da će, kako ovaj iterativni proces napreduje, očekivane vrednosti početi da konvergiraju ka tačnim vrednostima.
Naravno, ovo je samo grubi opis modela. Sve to ide malo finije, pošto se ceo problem analitički svede na par relativno jednostavnih samokonzistentih jednačina koje možeš numerički da rešiš.
Evo, pogledaj npr Phys. Rev. B 60, 1082–1099 (1999) (preprint:
http://arxiv.org/abs/cond-mat/9901027) - jedna od prvih referenci kada potražiš "self consistent spin wave theory na Google Scholar". Tu imaš ceo postupak za slojevite Hajzenbergove magnete.
#define TRUE FALSE /*Happy debugging suckers*/
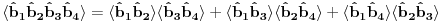
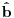 operatori bilo operatori anihilacije, bilo kreacije.
operatori bilo operatori anihilacije, bilo kreacije. 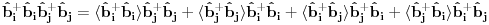
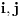 oznacavaju susedne cvorove. Kako se vrsi ovo dekuplovanje? Lici pomalo na gornju teoremu, ali nije. Ovo bi trebalo da se zove self consistent spin wave theory.
oznacavaju susedne cvorove. Kako se vrsi ovo dekuplovanje? Lici pomalo na gornju teoremu, ali nije. Ovo bi trebalo da se zove self consistent spin wave theory.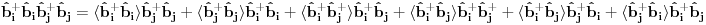 ?
? 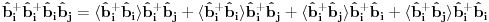
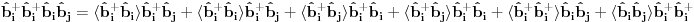




 Cvrsto stanje - pitanje
Cvrsto stanje - pitanje