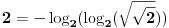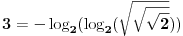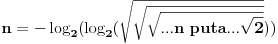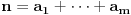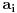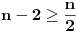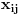Srodne teme

12.04.2002. zadaci
04.11.2004. Zadaci iz c++
04.07.2002. NRT na VETS
04.04.2004. Par pitanja o upisu na ETF
12.07.2003. zadaci razno
08.09.2003. Zadaci za ispite
30.11.2003. Zadaci za realni tip - potraga :)
12.09.2004. zadaci iz C-a?
15.03.2004. Zadaci iz PHP - a
06.03.2013. zadaci za prijemni iz matematike za Matematicku g..

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Najlepši zadaci

[es] :: Matematika :: Najlepši zadaci
(TOP topic)
Strane: << < .. 2 3 4 5 6 7 8 9 10 11 ... Dalje > >>

[ Pregleda: 317824 | Odgovora: 858 ] > FB > Twit

Autor

ast.
Nemanaj Djordjevic
Beograd

Član broj: 17559
Poruke: 2
*.matf.bg.ac.yu

Profil

Re: Najlepši zadaci

^{11.12.2003. u 14:12 - pre 260 meseci}

Citat:

Bojan Basic:
Trisekcija ugla je moguca sa greskom u najgorem slucaju 0.5% (dovoljno malo da bi bilo zanemarljivo, mada se malim usloznjavanjem postupka moze jos poboljsati, ako je potrebno). Za vikend cu napisati postupak u novoj temi.

Ma nije problem trisektirati ugao sa ocekivanom greskom, tako mozes da se zadovoljis i odokativnom metodom! Pazi josh je kao shto verovatno znash i cika Gaus dokazao da je to nemoguce i (to vrlo elegantno). Tuzno je sto je ona baka iz Nacija patentirala svoj "izum" kao apsolutni dokaz! Da bi ironija bila veca njen dokaz em shto je pogreshan em shto ona kao da zivi u neolitu! Pa ni stari grci se nisu zadovoljavali samo grafickim dokazom!
Ali dobro ona jadnica prica koliko zna!

Georg

Odgovor na temu

london
Wien-S.M.

Član broj: 18091
Poruke: 4
*.17.11.univie.teleweb.at

ICQ: 344844203

Profil

Re: Najlepši zadaci

^{24.12.2003. u 06:25 - pre 259 meseci}

Citat:

noviKorisnik:
Hvala na hintu...

Mornar 1 stavi kondom A.
Mornar 1 stavi kondom B.
Mornar 1 se zadovolji s prostitutkom.
Mornar 1 skine kondom B.
Mornar 1 skine kondom A.

Mornar 2 stavi kondom B.
Mornar 2 se zadovolji s prostitutkom.
Mornar 2 skine kondom B.

Mornar 3 izvrne kondom A.
Mornar 3 stavi kondom A.
Mornar 3 stavi kondom B.
Mornar 3 se zadovolji s prostitutkom.
Mornar 3 skine kondom B.
Mornar 3 skine kondom A.

Mornari baciše kondome na reciklažu, pozvaše prostitutku na čašicu ruma i pitaše je "da li si zadovoljena?

... čista hirurgija :D

[Ovu poruku je menjao london dana 24.12.2003. u 17:35 GMT]

i tako u beskrajno...

Odgovor na temu

noviKorisnik
Dejan Katašić
Novi Sad

Član broj: 13216
Poruke: 4533
*.bankmeridian.com

Sajt: www.novikorisnik.net

+5 Profil

Re: Najlepši zadaci

^{24.12.2003. u 06:55 - pre 259 meseci}

Antune, nemoj da zbunjuješ. Stavio si svoj komentar unutar citata, oči mi ispadoše dok nađoh

Citat:

Lepo resenje ako se zna da ONA ima sidu
ali u pitanju je spomenuto 4 osobe

Proveri još jednom, jeste čista hirurgija i sida ostaje tamo gde jeste.

BoxUp
interesantna logička igra
Monty Hall paradoks - interaktivni demo

Odgovor na temu

london
Wien-S.M.

Član broj: 18091
Poruke: 4
*.17.11.univie.teleweb.at

ICQ: 344844203

Profil

Re: Najlepši zadaci

^{24.12.2003. u 15:41 - pre 259 meseci}

Izvini Dejane na ubacivanju u citat.
Mislio sam da ce se sam odvojiti.
Stisnuo sam odgovor sa citatom i mislio da ce logicki da ih odvoji.
Nov sam ovde kao sto si mozda primetio.

i tako u beskrajno...

Odgovor na temu

noviKorisnik
Dejan Katašić
Novi Sad

Član broj: 13216
Poruke: 4533
*.bankmeridian.com

Sajt: www.novikorisnik.net

+5 Profil

Re: Najlepši zadaci

^{25.12.2003. u 14:30 - pre 259 meseci}

Citat:

london:
Izvini Dejane na ubacivanju u citat.
Mislio sam da ce se sam odvojiti.
Stisnuo sam odgovor sa citatom i mislio da ce logicki da ih odvoji.
Nov sam ovde kao sto si mozda primetio.

... ma to je najmanja frka

BoxUp
interesantna logička igra
Monty Hall paradoks - interaktivni demo

Odgovor na temu

blaza
n/a

Član broj: 961
Poruke: 743
*.vdial.verat.net

+3 Profil

Re: Najlepši zadaci

^{27.12.2003. u 18:37 - pre 259 meseci}

Citat:

Inace, sto se tice zadatka sa tri dvojke, sada je najzad sve jasno:

i uopste:

Moderator: tex

Ovo je resenje Pola Diraka, cuvenog fizicara nobelovca iz 1926. godine.

O_o

Odgovor na temu

BOOK
Beograd

Član broj: 9769
Poruke: 117
*.135.EUnet.yu

Jabber: BOOK@elitesecurity.org

Profil

Re: Najlepši zadaci

^{17.01.2004. u 22:56 - pre 258 meseci}

Oprosti, ali to je MOJE rešenje, bez obzira što je tamo neki pokojnik sasvim slučajno našao isto rešenje kao i ja...

Bojan Bašić: obrisan nepotreban citat

[Ovu poruku je menjao Bojan Basic dana 18.01.2004. u 01:10 GMT]

Odgovor na temu

BOOK
Beograd

Član broj: 9769
Poruke: 117
*.135.EUnet.yu

Jabber: BOOK@elitesecurity.org

Profil

Re: Najlepši zadaci

^{17.01.2004. u 23:02 - pre 258 meseci}

Evo još jedan lepotan:

Code:
Zadatak 20:

Svaki prirodan broj se na mnogo načina može predstaviti kao zbir drugih prirodnih
brojeva. Na primer, broj 5 se može napisati kao 1+1+1+1+1, 1+1+1+2, 1+1+3,
1+2+2, 1+4, 2+3 i najzad samo kao 5.

Naći za svaki prirodan broj (tj. naći opštu formulu) takvo rastavljanje na sabirke da
oni daju najveći mogući proizvod kada se pomnože. Na primer, u gornjem primeru to
je rastavljanje 5=2+3 (2*3=6).

p.s
Glava ću vam se ponaotkidati ako se budete uhvatili programiranja.

Odgovor na temu

blaza
n/a

Član broj: 961
Poruke: 743
*.vdial.verat.net

+3 Profil

Re: Najlepši zadaci

^{18.01.2004. u 05:49 - pre 258 meseci}

Citat:

BOOK:
Oprosti, ali to je MOJE rešenje, bez obzira što je tamo neki pokojnik sasvim slučajno našao isto rešenje kao i ja...

U redu je... ja sam samo napomenuo da je Pol Dirak prvi resio taj zadatak, a, kako si ti dosao do istog resenja, treba da si ponosan jer razmisljas kao cuveni nobelovac.

O_o

Odgovor na temu

Mihailo Kolundzija
Novi Sad

Član broj: 11323
Poruke: 100
*.dialup.ns.ac.yu

+1 Profil

Re: Najlepši zadaci

^{18.01.2004. u 06:35 - pre 258 meseci}

On Sun, 18 Jan 2004 00:02:07 CET, BOOK wrote:

Citat:

Code:
Zadatak 20:
Svaki prirodan broj se na mnogo načina može predstaviti kao zbir drugih
prirodnih
brojeva. Na primer, broj 5 se može napisati kao 1+1+1+1+1, 1+1+1+2, 1+1+3,
1+2+2, 1+4, 2+3 i najzad samo kao 5.

Naći za svaki prirodan broj (tj. naći opštu formulu) takvo rastavljanje na
sabirke da
oni daju najveći mogući proizvod kada se pomnože. Na primer, u gornjem
primeru to
je rastavljanje 5=2+3 (2*3=6).

Da pokušam:

Odgovor na temu

BOOK
Beograd

Član broj: 9769
Poruke: 117
*.216.EUnet.yu

Jabber: BOOK@elitesecurity.org

Profil

Re: Najlepši zadaci

^{18.01.2004. u 07:53 - pre 258 meseci}

Dobro si pokušao. Još kad bi rekao zašto bio bih jako srećan.

Odgovor na temu

stalker
Branko Kokanovic
Beograd

Član broj: 11897
Poruke: 606
*.rcub.bg.ac.yu

+2 Profil

Re: Najlepši zadaci

^{18.01.2004. u 10:11 - pre 258 meseci}

Pa, programiranjem:))))

Odgovor na temu

Mihailo Kolundzija
Novi Sad

Član broj: 11323
Poruke: 100
*.dialup.ns.ac.yu

+1 Profil

Re: Najlepši zadaci

^{18.01.2004. u 12:43 - pre 258 meseci}

On Sun, 18 Jan 2004 08:53:10 CET, BOOK wrote:

Citat:

Dobro si pokušao. Još kad bi rekao zašto bio bih jako srećan.

Šta ću - zadatak mi se učinio interesantnim, pa reko', 'ajd' da pokušam da
ga uradim. Eto zašto.

A ako te zanima dokaz zadatka, pokušaću i njega da dam. Prvo, postavka
zadatka me je odma' asocirala na dinamičko programiranje, al' reko', da ja
ipak sačuvam tikvu, i da se manem te jeresi u startu. Međutim, to mi je
dalo ideju da rastavljanje

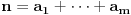
nije
optimalno u slučaju da se bilo koje

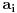
može predstaviti kao
suma prirodnih brojeva čiji je proizvod veći od njega samog (da ne bude
zabune, mislim na

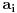
). Kako se svaki prirodan broj veći ili
jednak četiri može predstaviti na ovaj način, pošto je za njih, recimo,

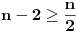
, to nam u igri ostaju samo brojevi 2 i
3, pošto za njih tak'o rastavljanje ne postoji (slučaj kad je n jednako
jedan je trivijalan, i ne uključuje nijedan od ova dva broja). Dalje, kako
je neopravdano imati više od dve dvojke u tom "rastavljanju", jerbo se
2+2+2 mož' zameniti sa 3+3, a da se dobije na proizvodu, to nam ostaje da
gomilamo trojke, a dvojke koristimo samo ako nam "pretekne". I tako, da ne
dužim, dobijem ono što sam napisao, sa dodatkom da se one dve dvojke
javljaju iz razloga što daju veći proizvod od trojke i jedinice (mada je i
jedna četvorka mogla da stoji umesto njih).

E sad, kad sam ja bar pokušao da dam nešto što bi se moglo nazvati
pokušajem dokaza, molio bih te da nas usrećiš sa dokazom onog zadatka sa
determinantom koji si rešio pre izvesnog vremena (pogledaj nekoliko poruka
pre ove), pošto mislim da će to zadatak učiniti mnogo zanimljivijim.

Na kraju za Branka, pošto sam video da se žali da nema neku tablicu
integrala - pogledaj ftp://shell.shore.net/members/w/s/ws/Support/cheat.pdf

Odgovor na temu

BOOK
Beograd

Član broj: 9769
Poruke: 117
*.23.EUnet.yu

Jabber: BOOK@elitesecurity.org

Profil

Re: Najlepši zadaci

^{18.01.2004. u 18:36 - pre 258 meseci}

Lepo si to objasnio. Iako nije sasvim formalno, rešenje se ipak vidi i to sasvim jasno. Zadatak je samo lep, nije uopšte težak :(

Što se tiče onog zadatka sa determinantom matrice, nisam mogao da odolim iskušenju jeresi :)

Odgovor na temu

Mihailo Kolundzija
Novi Sad

Član broj: 11323
Poruke: 100
*.dialup.ns.ac.yu

+1 Profil

Re: Najlepši zadaci

^{18.01.2004. u 23:32 - pre 258 meseci}

Dobro, sad videh da je bilo i nekih sitnih grešaka u onome što sam napisao,
ali to u suštini ne menja stvari. Možda se mogla primeniti i neka indukcija
kako bi se to dovelo u formalno prihvatljivu celinu, ali valjda nije baš
tol'ko loše ni u onakvom obliku.

Ako onaj zadatak sa determinantom više nikom nije zanimljiv za paćenje,
mogu da dostavim jedno elegantno rešenje, zbog kojeg sam ga baš i postavio
(inače, rešenje nije moje, pošto sam ja kao svako neinventivno i bezidejno
biće krenuo da se patim sa indukcijom, te mi je na kraju ponestalo
vremena). Doduše, baš zbog toga što sam očekivao odgovor kakav si dao,
razmišljao sam i da preformulišem zadatak u formu "dokazati da je ...
jednaka 1" , ali sam na kraju odustao.

I da nadovežem predlog da ako posle određenog vremena niko ne reši zadatak,
a onaj ko ga je postavio zna njegovo rešenje (znači, iz igre otpadaju
zlatni potoci i traženja pomoći), taj isti objavi rešenje kako bi možda
neko pokupio neku interesantnu ideju koja će mu možda jednog dana negde
biti od koristi (šta ćete, nikad se ne zna).

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu

+64 Profil

Re: Najlepši zadaci

^{28.01.2004. u 18:52 - pre 258 meseci}

Već na prvi pogled (tek juče sam ga video) zadatak sa matricom mi se mnogo svideo. Elegantan rezultat je još lepši ako je takvo i rešenje. Mihailo je pokazao već više puta svoje kvalitete u tom smislu. 'Ajd i ja da probam :

Ideja je da se matrica svede na trougaonu, gde su svi elementi ispod glavne dijagonale jednaki 0, a na samoj dijagonali su sve jedinice. (Ako već znamo da je determinanta jednaka 1 onda je ovako nešto sigurno moguće, ali naravno, ne mora da znači odmah da je to i najbolji put.)
Posle dosta raznih pokušaja, ispisivanja sve većih matrica, polako mi je sinulo. Postupak bi se mogao ovako opisati najjednostavnije :

svaku vrstu množimo sa -1 i dodajemo je svakoj sledećoj vrsti čiji indeks sadrži indeks ove koju dodajemo; npr. drugu vrstu, pomnoženu sa -1, dodajemo četvrtoj, šestoj, osmoj itd.... naravno ne moramo da teramo ovo sa svim vrstama, već do [n/2].

U čemu je trik? Svaka vrsta sadrži elemente koji pokazuju koliko njen indeks ima delitelja za odgovarajući indeks kolone. Ako smo prethodni postupak uradili za svaku vrstu-delitelja onda će odgovarajući element vrste biti 0 ako je indeks vrste i kolone različit a 1 ako se polapaju, jer se i sam broj računa kao svoj delitelj. Izuzetak su vrste čiji je indeks prost broj. Posle prvog prolaza, sa prvom vrstom (čiji su svi elementi 1), takve imaju 1 samo na mestima gde je indeks kolone sadržalac njihovog indeksa a ostalo su nule. Naravno prva jedinica se pojavljuje na glavnoj dijagonali. U ostatku postupka, ove vrste ostaju netaknute.

P.S. Osećam potrebu da dam konkretan primer, ali sad me nešto mrzucka. Ko prati uputstva, moći će lako da proveri.
//30.01.
Evo, pošto nema nikakvog komentara, primer :

U prvom potezu, prvom vrstom oduzimamo po jedan u svim ostalim. Drugu vrstu oduzimamo od četvrte i šeste, a treću od šeste.

Odgovor na temu

vandrija
Andrija Velimirovic
Beograd

Član broj: 20189
Poruke: 6
*.ptt.yu

Profil

Re: Najlepši zadaci

^{02.02.2004. u 23:11 - pre 258 meseci}

Da li neko ima resenje za zadatak 20 u C-u ili Pascal-u?

Odgovor na temu

BOOK
Beograd

Član broj: 9769
Poruke: 117
*.46.EUnet.yu

Jabber: BOOK@elitesecurity.org

Profil

Re: Najlepši zadaci

^{03.02.2004. u 11:41 - pre 258 meseci}

Nažalost, ovo moje je u Javi, ali program lako možeš prebaciti u C:

Code:

import java.io.*;
class E
{
public static void main (String[] args) throws IOException
  {
     BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
     int br = Integer.parseInt(bf.readLine());
     if (br<3)
     {
        System.out.println(br);
        return;
     }
     for (int i=1; i < br/3; i++) System.out.print("3 ");
     switch (br%3)
      {
         case 0: System.out.print("3 "); break;
         case 1: System.out.print("2 2 "); break;
         case 2: System.out.print("3 2 "); break;
      }
}

:)))))

Pretpostavljam da hoćeš program koji nalazi sva moguća rastavljanja i onda za svaki proverava proizvod, te štampa ono rastavljanje kod koga je najveći proizvod. Evo i tog programa (zajebano je, ali to je najjednostavnije što mi trenutno pada na pamet).

Code:

import java.io.*;

class Rastavljanje
{
    int x = 0;
    int niz[][];

    Rastavljanje(int[][] a)
    {
        niz = a;
    }

    void rec(int y, int m, int n, int od)
    {
        if (m==1)
        {
            niz[x][y] = n;
            x++;
            for (int k=0; k < y; k++) niz[x][k] = niz[x-1][k];
        }
        else
        {
            for (int s = od; s <= n/m; s++)
            {
                niz[x][y] = s;
                rec(y+1, m-1, n-s, s);
            }
        }
    }

    public static void main (String[] args) throws IOException
     {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        int br = Integer.parseInt(bf.readLine()), maxp = 0, est = 10000;
        int all[][][] = new int[br][][];
        for (int m = 1; m <= br; m++)
        {
            all[m-1] = new int[est][m];
            Rastavljanje oe = new Rastavljanje(all[m-1]);
            oe.rec(0, m, br, 1);
            all[m-1][est-1][0] = oe.x;
        }

        int pok[] = new int[0], size = 0;
        System.out.println("Evo ih sva rastavljanja:");
        for (int m = 1; m <= br; m++)
        {
            for (int i=0; i < all[m-1][est-1][0]; i++)
            {
                int pp = 1;
                for (int j=0; j < m; j++)
                {
                    System.out.print(all[m-1][i][j] + " ");
                    pp *= all[m-1][i][j];
                }
                System.out.println();
                if (maxp < pp)
                {
                    maxp = pp;
                    pok = all[m-1][i];
                    size = m;
                }
            }
        }
        System.out.println("Najveci proizvod je za:");
        for (int i=0; i<size; i++) System.out.print(pok[i] + " ");
        System.out.println();
    }
}

Napomena: program je spor, jer se broj rastavljanja astronomski povećava (već za broj 50 treba povećati "est").

Odgovor na temu

Mihailo Kolundzija
Novi Sad

Član broj: 11323
Poruke: 100
*.ftn.ns.ac.yu

+1 Profil

Re: Najlepši zadaci

^{04.02.2004. u 17:48 - pre 258 meseci}

Citat:

darkosos:
Evo, pošto nema nikakvog komentara, primer :

Darko, nećeš verovat', al' to je baš način na koji sam ja radio dotični zadatak. Međutim, potrebno je dokazati da se tim postupkom dobija trougaona matrica, što se može uraditi indukcijom, ali je pomalo komplikovano.
Elegantno rešenje kaže da se naša matrica dobija množenjem matrica X i Y, gde element matrice X (

) ima vrednost jedan ukoliko i deli j, a nula u suprotnom, dok element matrice Y (

) ima vrednost jedan ukoliko j deli i, a nula u suprontnom.
Kako je determinanta proizvoda dve matrice jednaka proizvodu determinanti tih matrica, to je i determinanta naše matrice jednaka jedan, pošto predstavlja proizvod gornje i donje-trougaone matrice koje na glavnoj dijagonali imaju samo jedinice.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.ptt.yu

+64 Profil

Re: Najlepši zadaci

^{04.02.2004. u 22:56 - pre 258 meseci}

Elegantno, nema šta!
Doduše nije ni indukcija baš toliki zalogaj. Ako su svi prethodni "sređeni", onda su kod složenih brojeva jedinice samo na glavnoj dijagonali, a kod prostih kako sam već opisao. Ako je naredni broj prost, onda je prosto :), a ako je složen, lako se vidi da iznad iman taman jedinica koliko treba.
U svakom slučaju, rešenje sa dve matrice koje se množe je odlično!

Odgovor na temu

[es] :: Matematika :: Najlepši zadaci
(TOP topic)
Strane: << < .. 2 3 4 5 6 7 8 9 10 11 ... Dalje > >>

[ Pregleda: 317824 | Odgovora: 858 ] > FB > Twit

Srodne teme

12.04.2002. zadaci
04.11.2004. Zadaci iz c++
04.07.2002. NRT na VETS
04.04.2004. Par pitanja o upisu na ETF
12.07.2003. zadaci razno
08.09.2003. Zadaci za ispite
30.11.2003. Zadaci za realni tip - potraga :)
12.09.2004. zadaci iz C-a?
15.03.2004. Zadaci iz PHP - a
06.03.2013. zadaci za prijemni iz matematike za Matematicku g..

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.