Za ovo prvo, nije prava p razlicita od prave q vec
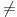
znaci da nemaju zajednickih tacaka (aka ne seku se).
1. (∀p)(∃q)(p=q ∧ p||q) p i q su prave
Za svaku pravu p postoji prava q takva da p i q nemaju zajednickih tacaka (ne seku se) i paralelne su.
2. (∃x∈Z)(∃y∈Z)(x+y=0)
Postoje x i y iz Z (Z je
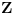
) tako da je x+y=0
3. (∃x∈R)(∀y∈R)(x+y=0)
Postoji realan broj x (dakle iz [tex]\mathbb{R}) tako da za svaki realan broj y vazi da je x+y=0
4. ¬(∀p,q)(∃A)(A∈p ∧ A∈q) p i q su prave, A je tacka
E da, nisam obratio paznju na ovo. Ovo ovde je DeMorganov zakon i vazi sledece:
(∃x)¬A ⇔ ¬(∀x)A i (∀x)¬A ⇔ ¬(∃x)A
Tako da se ova formula svodi na sledece:
¬(∀p,q)(∃A)(A∈p ∧ A∈q) ⇔ (∃p,q)¬(∃A)(A∈p ∧ A∈q) ⇔ (∃p,q)(∀A)¬(A∈p ∧ A∈q) ⇔ (∃p,q)(∀A) (A∉p ˅ A∉q)
Odnosno, postoje prave p i q takve da za svaku tacku A vazi da A ne pripada p ili A ne pripada q. Ovo bi znacilo da su prave paralelne (ako sam sve ovo pretumbao dobro do kraja)
DeMorganovi zakoni nam govore da negacija prolazi kroz kvantifikatore isto kao sto prolazi kroz konjukciju i disjunkciju
5. (∀x,y)(x∈Q ∧ y∈Q) ⇒ (x+y∈Q ∧ x·y∈Q)
Za svako x i y, takvo da x i y pripadaju Q sledi x+y pripada Q i x*y pripada Q
[Ovu poruku je menjao atomant dana 01.11.2010. u 20:15 GMT+1]
If you can't explain it simply, you don't understand it well enough. A. Einstein