Prvi korak je da transformišeš sistem tako da ima samo prve izvode, uvođenjem smene
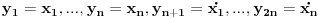
. Zatim na levoj strani ostaviš samo prve izvode
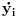
, a ostalo prebaciš na desnu i izdvojiš koeficijente uz
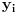
. Tada desnu stranu možeš da izraziš kao proizvod matrice poznatih koeficijenata i vektora
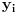
, pa sabrano sa još jednim poznatim vektorom, tako da ispadne
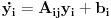
. Na to se dodaju jednačine usled smena
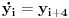
, pa još ako odbacimo indekse, ispadne matrična jednačina
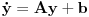
. Sada možeš da upotrebiš bilo koju metodu za numeričko rešavanje ovakvog sistema, najjednostavnije
Ojlerovu, ili mnogo tačniju
Runge-Kutinu četvrtog reda. (Ove dve su najpopularnije, a Njumarkova je koliko vidim negde između po složenosti i tačnosti, ne znam da li ima neku prednost u ovom kontekstu.) Ako je
indeks vremenskog trenutka, a
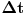
vremenski korak, Ojlerova metoda primenjena na ovaj sistem glasila bi:
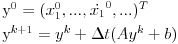
a Runge-Kutina četvrtog reda:
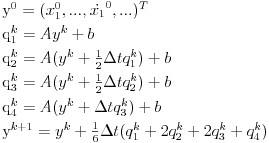
Ovako bi to izgledalo u pitonu (možda sam dobro presložio koeficijente, a možda i nisam), za nulte početne uslove i nulto
:
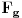
Code:
# -*- coding: UTF-8 -*-
from numpy import matrix
# Sistem ODJ prvog reda y' = A y + b.
A = matrix([
[0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 1],
[(-6000 -5000)/7.0, (+5000)/7.0, (+6000)/7.0, 0, (-250 -600)/7.0, (+600)/7.0, (+250)/7.0, 0],
[(+5000)/6.0, (-9000)/6.0, (-5000 +9000)/6.0, 0, (+600)/6.0, (-600)/6.0, 0, 0],
[(-6000)/14.0, (-9000)/14.0, (+6000 +9000 -25000)/14.0, (+25000)/14.0, (-250)/14.0, 0, (+250 -1700)/14.0, (+1700)/14.0],
[0, 0, (+25000)/45.0, (-25000)/45.0, 0, 0, (+1700)/45.0, (-1700)/45.0],
])
Fg = 0.0
b = matrix([
0.0,
0.0,
0.0,
0.0,
(+68.67 -Fg)/7.0,
(+58.86)/6.0,
(+137.34)/14.0,
(+441.45)/45.0,
]).transpose()
# Početni uslovi.
y0 = matrix([
# Početni položaji: x_1|0, ..., x_4|0.
0.0,
0.0,
0.0,
0.0,
# Početne brzine: x_1'|0, ..., x_4'|0.
0.0,
0.0,
0.0,
0.0,
]).transpose()
# Parametri integracije.
end_time = 1.0
num_steps = 100
dt = end_time / num_steps
print u"Krajnje vreme: %g" % end_time
print u"Broj koraka: %d" % num_steps
print u"Korak: %g" % dt
# Ojlerova metoda.
print u"Integralim..."
y_eu = y0
for k in range(num_steps):
y_eu = y_eu + dt * (A * y_eu + b)
print u"Konačni položaji i brzine Ojlerovom metodom:"
print y_eu
# Runge-Kutina metoda četvrtog reda (R-K 4).
print u"Integralim..."
y_rk4 = y0
for k in range(num_steps):
q1 = A * y_rk4 + b
q2 = A * (y_rk4 + 0.5 * dt * q1) + b
q3 = A * (y_rk4 + 0.5 * dt * q2) + b
q4 = A * (y_rk4 + dt * q3) + b
y_rk4 = y_rk4 + (1.0 / 6) * dt * (q1 + 2 * q2 + 2 * q3 + q4)
print u"Konačni položaji i brzine metodom R-K 4:"
print y_rk4
Ako se korak integracije smanjuje (tj. povećava krajnje vreme ili smanjuje broj koraka), rezultat će očekivano polako gubiti na tačnosti, ali će takođe pri određenom prevelikom koraku potpuno „odlepiti“ (izvršiti program za brojeve koraka npr. 50 i 60). To je tzv. granica stabilnosti za eksplicitne metode (kakve su i Ojlerova i R-K 4), i zavisi od jednačine koja se rešava.
Numericka metoda resavanja diferencijalnih jednacina
