Rekao bih da ovde neko drugi demonstrira svoje neznanje.
1. Polje realnih brojeva je bilo koje izabrano kompletno uređeno polje.
Kompletno uređeno polje je jedinstveno do na izomorfizam.
Najveći negativan realan broj ne postoji.
2. Nestandardna analiza je alternativno zasnivanje matematičke analize koje
ne počiva na realnim brojevima, tj. kompletnom uređenom polju, već na
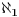
zasićenom uređenom polju (za model se obično uzima ultrastepen polja realnih brojeva na prebrojiv beskonačan skup, recimo N), koje zbog zasićenosti ne može biti arhimedovsko, pa samim tim ni kompletno uređeno polje, tj. to nije polje realnih brojeva. No, u tom polju takođe ne postoji najveći negativan element. Štaviše,
Niti jedno uređeno polje nema najveći negativan element, jer su uređena polja uvek karakteristike 0, pa se npr. dvojkom može deliti i uvek zadovoljavaju zakon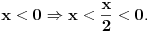 
Ovim si potpisao svoje nerazumevanje matematike. Matematički iskazi imaju precizno definisano značenje. Da si pitao "koji je najveći negativan element uređenog polja", formulacija bi sintaksno gledano bila nedorečena, jer nisi rekao na koje uređeno polje misliš, mada bi u ovom slučaju bila smislena, jer je odgovor isti za sva uređena polja
U proizvoljnom uređenom polju ne postoji najveći negativan element.
Tako da nemoj svoje frljanje da pripisuješ matematici. Ako si se već uhvatio za netandardnu analizu, tamo ne postoji -0, već
neprebrojivo beskonačno mnogo negativnih elemenata beskonačno bliskih nuli.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Re: Nula na nulti stepen daje jedinicu, jos jedan sjajan bug
